Conical stratifications via semialgebraic sets

The goal of this post is to describe a conical stratification of $\Ran_{\leqslant n}(M)\times \R_{\geqslant 0}$ that refines the stratification previously seen (in "Exit paths, part 2," 2017-09-28, and "Refining stratifiations," 2018-03-11). Thanks to Shmuel Weinberger for the key observation that the strata under consideration are nothing more than semialgebraic sets, which are triangulable, and so admit a conical stratification via this triangulation.

Remark: Fix $n\in \Z_{>0}$, let $M$ be a smooth, compact, connected, embedded submanifold in $\R^N$, and let $M^n$ have the Hausdorff topology. We will be interested in $M^n\times \R_{>0}$, though this will be viewed as the compact set $M^n\times [0,K]\subseteq \R^{nN+1}$ for some $K$ large enough (for instance, larger than the diameter of $M$) when necessary. The point 0 is added for compactness.

Stratification of the Ran space by semialgebraic sets

We begin by stratifying $M^n\times \R_{>0}$ by a poset $A$, creating strata based on the pairwise distance between points in each $M$ component. Then we take that to a stratification of the quotient $\Ran^{\leqslant n}(M)\times \R_{>0}$ via the action of the symmetric group $S_n$ and overcounting of points.

Definition: Define a partial order $\leqslant$ on the set $A = \big\{$partitions of ($\{1,\dots,n\}^2\setminus \Delta)/S_2$ into 4 parts$\big\}$ of ordered 4-tuples of sets by \[ (Q,R,S,T) \leqslant \left(Q\setminus Q',\ R\cup Q' \cup S',\ S\setminus (S'\cup S''),\ T\cup S''\right), \] for all $Q'\subseteq Q$ and $S',S''\subseteq S$, with $S'\cap S'' = \emptyset$.

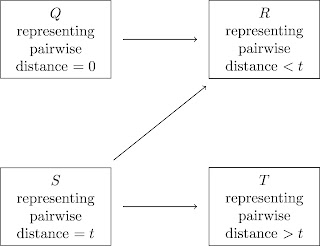
The diagram to keep in mind is the one below, with arrows pointing from lower-ordered elements to higher-ordered elements. Once we pass to valuing the 4-tuple in simplicial complexes, moving between $Q$ and $R$ will not change the simplicial complex type (this comes from the definition of the Vietoris--Rips complex).

Lemma 1: The map $f: M^n\times \R_{>0}\to (A,\leqslant)$ defined by \begin{align*} (\{P_1,\dots,P_n\},t)\mapsto \bigg( \{(i,j>i)\ & :\ P_i=P_j\},\ \{(i,j>i)\ :\ d_M(P_i,P_j)<t\},\\
& \{(i,j>i)\ :\ d_M(P_i,P_j)=t\},\ \{(i,j>i)\ :\ d_M(P_i,P_j)>t\}\bigg) \end{align*} is continuous in the upset topology on $(A,\leqslant)$.

Proof: Choose $(Q,R,S,T)\in A$ and consider the open set $U = U_{(Q,R,S,T)}$ based at $(Q,R,S,T)$. Take $(P,t)\in f^{-1}(U)$, which we claim has a small neighborhood still contained within $f^{-1}(U)$. If we move a point $P_i$ slightly that was exactly distance $t$ away from $P_j$, then the pair $(i,j)$ was in $S$, but is now in either $R$ or $T$, and both $(Q,R\cup\{(i,j)\},S\setminus \{(i,j)\},T)$ and $(Q,R,S\setminus \{(i,j)\},T\cup \{(i,j)\})$ are ordered higher than $(Q,R,S,T)$, so the perturbed point is still in $f^{-1}(U)$. If $P_i=P_j$ in $P$ and we move them apart slightly, since $t\in \R_{>0}$, the pair $(i,j)$ will move from $Q$ to $R$, and $(Q,R,S,T) \leqslant (Q\setminus \{(i,j)\},R\cup \{(i,j)\},S,T)$, so the perturbed point is still in $f^{-1}(U)$. For all pairs $(i,j)$ in $R$ or $T$, the distances can be changed slightly so that the pair still stays in $R$ or $T$, respectively. Hence $f$ is continuous. $\square$

This shows that $M^n\times \R_{>0}$ is stratified by $(A,\leqslant)$, using Lurie's definition of a (poset) stratification, which just needs a continuous map to a poset. Our goal is to work with the Ran space of $M$, instead of the $n$-fold product of $M$, which are related by the natural projection map $\pi : M^n\to \Ran^{\leqslant n}(M)$, taking $P=\{P_1,\dots,P_n\}$ to the unordered set of distinct elements in $P$. We also would like to stratify $\Ran^{\leqslant n}(M)\times \R_{>0}$ by simplicial complex type, so we need the following map.

Definition: Let $g: (A,\leqslant)\to SC$ be the map into simplicial complexes that takes $(Q,R,S,T)$ to the clique complex of the simple graph $C$ on $n-k$ vertices, for $|Q|=k(k+1)/2$, defined as follows: 

• $V(C) = \{[i]\ :\ i=1,\dots,n,\ [j]= [i] \text{\ iff\ } (i,j)\in Q\}$,
• $E(C) = \{([i],[j])\ :\ (i,j)\in R\cup S\}$.

We require $C$ to be simple, so if $(i,j)\in Q$ and $(i,\ell),(j,\ell)\in R\cup S$, we only add one edge $([i],[\ell])=([j],[\ell])$ to $C$.

The map $g$ induces a partial order $\leqslant$ on $SC$ from the partial order on $A$, with $C\leqslant C'$ in $SC$ whenever there is $(Q,R,S,T)\in g^{-1}(C)$ and $(Q',R',S',T')\in g^{-1}(C')$ such that $(Q,R,S,T) \leqslant (Q',R',S',T')$ in $A$. Note that if $C\in SC$ is not in the image of $g$, then it is not related to any other element of $SC$. By the universal property of the quotient and continuity of $f$ and $g$ (as $A$ and $SC$ are discrete), there is a continuous map $h:\Ran^{\leqslant n}(M)\times \R_{>0}\to (SC,\leqslant)$ such that the diagram

commutes. Hence $\Ran^{\leqslant n}(M)\times \R_{>0}$ is stratified by $(SC,\leqslant)$.

Remark: The map $\pi$ can be thought of as a quotient by the action of the symmetric group $S_n$, followed by the quotient of the equivalence relation \[ \{P^1_1,\dots,P^{\ell_1}_1,P^1_2,\dots,P^{\ell_2}_2,P^1_3,\dots,P^{\ell_k}_k\} \ \ \sim\ \
\{P^1_1,\dots,P^{\ell_1-1}_1,P^1_2,\dots,P^{\ell_2+1}_2,P^1_3,\dots,P^{\ell_k}_k\} \] on $M^n$, for all possible combinations $\ell_1+\cdots + \ell_k =n$ and $1\leqslant k\leqslant n-1$, where $P_m^i=P_m^j$ for all $1\leqslant i<j\leqslant \ell_m$.

Semialgebraic geometry

Next we move into the world of semialgebraic sets and triangulations, following Shiota. Here we come across a more restrictive notion of stratification of a manifold $X$, which requires a partition of $X$ into submanifolds $\{X_i\}$. If Lurie's stratification $f:X\to A$ gives back submanifolds $\{f^{-1}(a)\}_{a\in A}$, then we have Shiota's stratification. Conversely, the poset $(\{X_i\},\leqslant)$, for $X_i \leqslant X_j$ iff $X_i \subseteq \closure(X_j)$ is always a stratification in the sense of Lurie.

Definition 2: A semialgebraic set in $\R^N$ is a set of the form \[ \bigcup_{\text{finite}} \{x\in \R^N\ :\ f_1(x)=0,f_2(x)>0,\dots,f_m(x)>0\},\] for polynomial functions $f_1,\dots,f_m$ on $\R^N$. A semialgebraic stratification of a space $X\subseteq \R^N$ is a partition $\{X_i\}$ of $X$ into submanifolds that are semialgebraic sets.

Next we observe that the strata of $M^n\times \R_{>0}$ are semialgebraic sets, with the preimage theorem and I.2.9.1 of Shiota, which says that the intersection of semialgebraic sets is semialgebraic. Take $(Q,R,S,T)\in A$  and note that \[ f^{-1}(Q,R,S,T) = \left\{(\{P_1,\dots,P_n\},t)\in M^n\times \R_{>0}\ :\ \begin{array}{r l}
d(P_i,P_j) = 0 & \forall (i,j)\in Q,\\
t-d(P_i,P_j) = 0 & \forall (i,j)\in S, \\
t-d(P_i,P_j) > 0 & \forall (i,j)\in R, \\
d(P_i,P_j) - t > 0 & \forall (i,j)\in T.
\end{array}\right\} \] Here $d$ means distance on the manifold, and we assume the metric to be analytic. Alternatively, $d$ could be Euclidean distance between points on the embedding of $M^n\times \R_{>0}$, induced by the assumed embedding of $M$.

For his main Theorem II.4.2, Shiota uses cells, but we opt for simplices instead, and for cell complexes we use simplicial complexes. Every cell and cell complex admits a decomposition into simplicial complexes, even without introducing new 0-cells (by Lemma I.3.12), so we do not lose any generality.

Definition 3: Let $X,Y$ be semialgebraic sets.

• A map $f: X\to Y$ is semialgebraic if the graph of $f$ is semialgebraic.
• A semialgebraic cell triangulation of a semialgebraic set $X$ is a pair $(C,\pi)$, where $C$ is a simplicial complex and $\pi: |C|\to X$ is a semialgebraic homeomorphism for which $\pi|_{\interior(\sigma)}$ is a diffeomorphism onto its image.
• A semialgebraic cell triangulation $(C,\pi)$ is compatible with a family $\{X_i\}$ of semialgebraic sets if $\pi(\interior(\sigma))\subseteq X_i$ or $\pi(\interior(\sigma))\cap X_i = \emptyset$ for all $\sigma\in C$ and all $X_i$.

A semialgebraic cell triangulation $(C,\pi)$ of $X$ induces a stratification $X\to (C_0 \cup \{\pi(\interior(\sigma))\},\leqslant)$, where the order is the one mentioned just before Definition 2. We use the induced stratification and the cell triangulation interchangeably, specifically in Proposition 4.

A compatible conical stratification

Finally we put everything together to get a conical stratification of $\Ran^{\leqslant n}(M)\times \R_{>0}$. Unfortunately we have to restrict ourselves to piecewise linear manifolds, or PL manifolds, which are homeomorphic images of geometric realizations of simplicial complexes, as otherwise we cannot claim $M$ is a semialgebraic set. We can also just let $M=\R^k$, as the point samples we are given could be coming from an unknown space.

Proposition 4: Let $M$ be a PL manifold embedded in $\R^N$. There is a conical stratification $\widetilde h:\Ran^{\leqslant n}(M)\times \R_{>0}\to (B,\leqslant)$ compatible with the stratification $h: \Ran^{\leqslant n}(M)\times \R_{>0}\to (SC,\leqslant)$.

Proof: (Sketch) The main lifting is done by Theorem II.4.2 of Shiota. Since $M$ is PL, it is semialgebraic, and so $M^n\times \R_{>0}\subseteq \R^{nN+1}$ is semialgebraic, by I.2.9.1 of Shiota. Since the quotient $\pi$ of diagram (1) is semialgebraic, the space $\Ran^{\leqslant n}(M)\times \R_{>0}$ is semialgebraic, by Scheiderer. Similarly, $\{f^{-1}(a)\}_{a\in A}$ is a family of semialgebraic sets, where $f$ is the map from Lemma 1.  Theorem II.4.2 gives that $\Ran^{\leqslant n}(M)\times \R_{>0}$ admits a cell triangulation $(K,\tau)$ compatible with $\{h^{-1}(S)\}_{S\in SC}$. By the comment after Definition \ref{semialgdef}, this means we have a stratification $\Ran^{\leqslant n}(M)\times \R_{>0}\to (K_0\cup \{\tau(\interior(\sigma))\}_{\sigma\in K},\leqslant)$. Further, by Proposition A.6.8 of Lurie, we have a conical stratification $|K|\to (B,\leqslant)$. This is all described by the solid arrow diagram below.

The vertical induced map comes as the poset $B$ has the exact same structure as the abstract suimplicial complex $K$. The diagonal induced map comes as the map $|K|\to \Ran^{\leqslant n}(M)\times \R_{>0}$ is a homeomorphism, and so has a continuous inverse. Composing the inverse with the conical sratification of Lurie, we get a conical stratification of $\Ran^{\leqslant n}(M)\times \R_{>0}$. Composing the vertical induced arrow and the maps to $(SC,\leqslant)$ show that there is a conical stratification of $\Ran^{\leqslant n}\times \R_{>0}$ compatible with its simplicial complex stratification from diagram (1). $\square$

Shiota actually requires that the space that admits a triangulation be closed semialgebraic, and having $\R_{>0}$ violates that condition. Replacing this piece with $\R_{\geqslant 0}$, then applying Shiota, and afterwards removing the $t=0$ piece we get the same result.

Remark: Every (sufficiently nice) manifold admits a triangulation, so it may be possible to extend this result to a larger class of manifolds, but it seems more sophisticated technology is needed.

References: Shiota (Geometry of subanalytic and semialgebraic sets, Chapters I.2, I.3, II.4), Scheiderer (Quotients of semi-algebraic spaces), Lurie (Higher algebra, Appendix A.6)