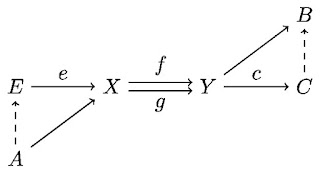A naive constructible sheaf

In this post we describe a constructible sheaf over $X=\Ran^{\leqslant n}(M)\times \R_{>0}$ valued in simplicial complexes, for a compact, smooth, connected manifold $M$. We note however that it does not capture all the information about the underlying space. Thanks to Joe Berner for helpful ideas.

Recall the category $SC$ of simplicial complexes and simplicial maps, as well as the full subcategories $SC_n$ of simplicial complexes with $n$ vertices (the vertices are unordered). Let $A = \bigcup_{k=1}^n SC_n$ with the ordering $\leqslant_A$ as in a previous post ("Ordering simplicial complexes with unlabeled vertices," 2017-12-03), and $f:X\to A$ the stratifying map. Let $\{A_k\}_{k=1}^N$ be a cover of $X$ by nested open sets of the type $f^{-1}(U_S) = f^{-1}(\{T\in A\ :\ S\leqslant_A T\})$, whose existence is guaranteed as $A$ is finite. Note that $f(A_1)$ is a singleton containg the complete simplex on $n$ vertices.

Remark: For every simplicial complex $S\in A$, there is a locally constant sheaf over $f^{-1}(S)\subseteq X$. Given the cover $\{A_k\}$ of $X$, denote this sheaf by $\mathcal F_k \in \Shv(A_k\setminus A_{k-1})$ and its value by $S_k\in SC$.

Let $i^1:A_1\hookrightarrow A_2$ and $j^2:A_2\setminus A_1 \hookrightarrow A_2$ be the natural inclusion maps . Note that $A_1$ is open and $A_2\setminus A_1$ is closed in $A_2$. The maps $i^1,j^2$ induce direct image functors on the sheaf categories $$i^1_*:\Shv(A_1) \to \Shv(A_2), \hspace{1cm} j^2_*:\Shv(A_2\setminus A_1) \to \Shv(A_2).$$ The induced sheaves in $\Shv(A_2)$ are extended by 0 on the complement of the domain from where they come. Note that since $A_2\setminus A_1\subseteq A_2$ is closed, $j^2_*$ is the same as $j^2_!$, the direct image with compact support. We then have the direct sum sheaf $i^1_*\mathcal F_1 \oplus j_*^2\mathcal F_2 \in \Shv(A_2)$, which we interpret as the disjoint union in $SC$. Then $$\left(i_*^1\mathcal F_1 \oplus j_2^*\mathcal F_2\right)(U) = \begin{cases} S_1 & \text{ if }U\subseteq A_1, \\ S_2 & \text{ if }U\subseteq A_2\setminus A_1, \\ S_1\sqcup S_2 & \text{ else,} \end{cases} \hspace{1cm} \left(i_*^1\mathcal F_1 \oplus j_2^*\mathcal F_2\right)_{(P,t)} = \begin{cases} S_1 & \text{ if } (P,t)\in A_1, \\ S_2 & \text{ if }(P,t)\in \text{int}(A_2\setminus A_1), \\ S_1\sqcup S_2 & \text{ else,} \end{cases}$$ for $U\subseteq A_2$ open and $(P,t)\in A_2$. Generalizing this process, we get a sheaf on $X$. The diagram

may be helpful to keep in mind. We use the fact that direct sums commute with colimits (used in the definition of the direct image sheaf) to simplify notation. We then get sheaves $$\begin{array}{r c l} \mathcal F^1 & \in & \Shv(A_1), \\ i_*^1\mathcal F^1 \oplus j_*^2 \mathcal F^2 & \in & \Shv(A_2), \\ i_*^2i_*^1\mathcal F^1 \oplus i_*^2j_*^2 \mathcal F^2 \oplus j_*^3 \mathcal F^3 & \in & \Shv(A_3), \\ i_*^3i_*^2i_*^1\mathcal F^1 \oplus i_*^3i_*^2j_*^2 \mathcal F^2 \oplus i_*^3j_*^3 \mathcal F^3 \oplus j_*^4 \mathcal F^4 & \in & \Shv(A_4), \end{array}$$ and finally $$i_*^{N-1\cdots 1}\mathcal F^1 \oplus \left(\bigoplus_{k=2}^{N-1} i_*^{N-1\cdots k}j_*^k \mathcal F^k \right) \oplus j_*^N \mathcal F^N \in \Shv(A_N=X),$$ where $i_*^{N-1\cdots k}$ is the composition $i_*^{N-1} \circ i_*^{N-2} \circ \cdots \circ i_*^k$ of direct image functors. Call this last sheaf simply $\mathcal F \in \Shv(X)$. Each $i_*^k$ extends the sheaf by 0 on an ever larger domain, so every summand in $\mathcal F$ is non-zero on exactly one stratum as defined by $f:X\to A$. We now have a functor $\mathcal F:Op(X) \to SC$ defined by $$\mathcal F(U) = \bigsqcup_{k=1}^N S_k \delta_{U,A_K\setminus A_{k-1}}, \hspace{1cm} \mathcal F_{(P,t)} = \bigsqcup_{k=1}^N S_k \delta_{(P,t),\text{cl}(,A_K\setminus A_{k-1})},$$ where $\delta_{U,V}$ is the Kronecker delta that evaluates to the identity if $U\cap V \neq \emptyset$ and zero otherwise.

Remark: The sheaf $\mathcal F$ is $A$-constructible, as $\mathcal F|_{f^{-1}(S)}$ is a constant sheaf evaluating to the simplicial complex $S\in A$. However, if we want the cohomology groups to capture how the simplicial complexes change between strata, then we must use a different approach - all groups die when leaving a stratum because of the extension by zero construction.

References: nLab (article "Simplicial complexes")

Sheaves, derived and perverse

Let $X,Y$ be topological spaces and $f:X\to Y$ a continuous map. We let $\Shv(X)$ be the category of sheaves on $X$, $D(\Shv(X))$ the derived category of sheaves on $X$, and $D_b(\Shv(X))$ the bounded variant. Recall that $D(\mathcal A)$ for an abelian category $\mathcal A$ is constructed first by taking $C(\mathcal A)$, the category of cochains of elements of $\mathcal A$, quotienting by chain homotopy, then quotienting by all acylic chains.

Remark: Let $\mathcal F\in \Shv(X)$. Recall:

• a section of $\mathcal F$ is an element of $\mathcal F(U)$ for some $U\subseteq X$,
• a germ of $\mathcal F$ at $x\in X$ is an equivalence class in $\{s\in \mathcal F(U)\ :\ U\owns x\}/\sim_x$,
• $s\sim_x t$ iff every neighborhood $W$ of $x$ in $U\cap V$ has $s|_W = t|_W$, for $s\in \mathcal F(U)$, $t\in \mathcal F(V)$,
• the support of the section $s\in\mathcal F(U)$ is $\supp(s) = \{x\in U\ :\ s \nsim_x 0\}$,
• the support of the sheaf $\mathcal F$ is $\supp(\mathcal F) = \{x\in X\ :\ \mathcal F_x\neq 0\}$.

Definition: The map $f$ induces functors between categories of sheaves, called
$$\begin{array}{r r c l} \text{direct image} & f_*\ :\ \Shv(X) & \to & \Shv(Y), \\ & (U\mapsto \mathcal F(U)) & \mapsto & (V\mapsto \mathcal F(f^{-1}(V))),\\[15pt] \text{inverse image} & f^*\ :\ \Shv(Y) & \to & \Shv(X), \\ & (V\mapsto \mathcal G(V)) & \mapsto & \text{sh}\left(U\mapsto \text{colim}_{V\supseteq f(U)} \mathcal G(V)\right),\\[15pt] \text{direct image with compact support} & f_!\ :\ \Shv(X) & \to & \Shv(Y), \\ & (U\mapsto \mathcal F(U)) & \mapsto & \left(V\mapsto \left\{ s\in\mathcal F(f^{-1}(V))\ :\ f|_{\supp(s)} \text{ is proper}\right\}\right). \end{array}$$

Above we used that $f:X\to Y$ is proper if $f^{-1}(K)\subseteq X$ is compact, for every $K\subseteq Y$ compact. Next, recall that a functor $\varphi:\mathcal A\to \mathcal B$ induces a functor $R\varphi:D(\mathcal A)\to D(\mathcal B)$, called the (first) derived functor of $\varphi$, given by $R\varphi(A^\bullet) = H^1(\varphi(A)^\bullet)$.

Remark: Each of the maps $f_*,f^*,f_!$ have their derived analogues $Rf_*, Rf^*,Rf_!$, respectively. For reasons unclear, $Rf_!$ has a right adjoint, denoted $Rf^!:D(\Shv(Y))\to D(\Shv(X))$. This is called the exceptional inverse image.

We are now ready to define perverse sheaves.

Definition: Let $A^\bullet \in D(\Shv(X))$. Then:

• the $i$th cohomology sheaf of $A^\bullet$ is $H^i(A^\bullet) = \ker(d^i)/\im(d^i)$,
• $A^\bullet$ is a constructible complex if $H^i(A^\bullet)$ is a constructible sheaf for all $i$,
• $A^\bullet$ is a perverse sheaf if $A^\bullet\in D_b(\Shv(X))$ is constructible and $\dim(\supp(H^{-i}(P))) \leqslant i$ for all $i\in \Z$ and for $P=A^\bullet$ and $P=(A^\bullet)^\vee = (A^\vee)^\bullet$ the dual complex of sheaves.

We finish off with an example.

Example: Let $X = \R$ be a stratified space, with $X_0=0$ the origin and $X_1 = \R\setminus 0$. Let $\mathcal F\in \Shv(X)$ be an $\R$-valued sheaf given by $\mathcal F(U) = \inf_{x\in U} |x|$, and define a chain complex $A^\bullet$ in the following way:
$$0 \longrightarrow A^{-1} = \mathcal F \xrightarrow{ d^{-1}=\text{id} } A^0 = \mathcal F \xrightarrow{ d^0=0 } 0.$$
Note that for any $U\subseteq \R$, we have $H^{-1}(A^\bullet)(U) = \ker(d^{-1})(U) = \ker(\id:\mathcal F(U)\to \mathcal F(U)) = \emptyset$ if $0\not\in U$, and $0$ otherwise. Hence $\supp(H^{-1}(A^\bullet)) = \R\setminus 0$, whose dimension is 1. Next, $H^0(A^\bullet)(U) = \ker(d^0)(U)/\im(d^{-1})(U) = \ker(0:\mathcal F(U)\to 0)/\im(\id:\mathcal F(U)\to \mathcal F(U)) = \mathcal F(U)/\mathcal F(U) = 0$, and so $\dim(\supp(H^0(A^\bullet))) = 0$. Note that $A^\bullet$ is self-dual and constructible, as the cohomology sheaves are locally constant. Hence $A^\bullet$ is a perverse sheaf.

References: Bredon (Sheaf theory, Chapter II.1), de Catalado and Migliorini (What is... a perverse sheaf?), Stacks project (Articles "Supports of modules and sections" and "Complexes with constructible cohomology")

Ordering simplicial complexes with unlabeled vertices

The goal of this post is to describe a partial order on the collection of simplical complexes with $\leqslant n$ unlabeled vertices that is nice in the context of the space $X=\Ran^{\leqslant n}(M)\times \R_{>0}$.

First note that there is a natural order on (abstract) simplicial complexes, given by set inclusion. Interpreting elements of $X$ as simplicial complexes induces a more restrictive order, as new vertices must "split off" from existing ones rather than just be introduced anywhere. Also note that the category usually denoted by $SC$ of simplicial complexes and simplicial maps contains objects with unordered vertices. Here we assume an order on them and consider the action of the symmetric groups to remove the order.

Definition: Let $SC_k$, for some positive integer $k$, be the collection of simplicial complexes with $k$ uniquely labeled vertices. This collection is a poset, with $S\leqslant T$ iff $\sigma\in T$ for every $\sigma\in S$.

The symmetric group on $k$ elements acts on $SC_k$ by permuting the vertices, and taking the image under this action we get $SC_k/S_k$, the collection of simplicial complexes with $k$ unlabeled vertices. This set also has a partial order, with $S\leqslant T$ in $SC_k/S_k$ iff $S'\leqslant T'$ in $SC_k$, for some $S'\in q_k^{-1}(S)$ and $T'\in q_k^{-1}(T)$, where $q_k:SC_k \twoheadrightarrow SC_k/S_k$ is the quotient map.

Definition: For all $i=1,\dots,k$, let $s_{k,i}$ be the $i$th splitting map, which splits the $i$th vertex in two. That is, if the vertices of $S\in SC_k$ are labeled $v_1,\dots,v_k$, then $s_{k,i}$ is defined by
$$\begin{array}{r c l} s_{k,i}\ :\ SC_k & \to & SC_{k+1}, \\ S & \mapsto & \left\langle S'\cup \{v_i,v_{i+1}\} \cup \displaystyle \bigcup_{\{v_i,w\}\in S'} \{v_{i+1},w\} \right\rangle , \end{array}$$ where $S'$ is $S$ with $v_j$ relabeled as $v_{j+1}$ for all $j>i$, and $\langle T\rangle$ is the simplicial complex generated by $T$.

By "generated by $T$" we mean generated in the Vietoris-Rips sense, that is, if $\{v_a,v_b\}\in T$ for all $a,b$ in some indexing set $I$, then $\{v_c\ :\ c\in I\}\in \langle T\rangle$. The $i$th splitting map is essentially the $i$th face map used for simplicial sets.

Let $A = \bigcup_{k=1}^n SC_k/S_k$. The splitting maps induce a partial order on $A$, with $S\leqslant T$, for $S\in SC_k/S_k$ and $T\in SC_{k+1}/S_{k+1}$, iff $s_{k,i}(S')\leqslant T'$ in $SC_k$, for some $S'\in q_k^{-1}(S)$, $T'\in q_{k+1}^{-1}(T)$, and $i\in \{1,\dots,k\}$. This generalizes via composition of the splitting maps to any pair $S,T\in A$, and is visually decribed by the diagram below.

Now, let $M$ be a smooth, compact, connected manifold embedded in $\R^N$, and $X=\Ran^{\leqslant n}(M)\times \R_{>0}$. Let $f:X\to A$ be given by $(P,t)\mapsto VR(P,t)$, the Vietoris-Rips complex around the points of $P$ with radius $t$.

Proposition: The map $f:X\to A$ is continuous.

Proof: Let $S\in A$ and $U_S \subseteq A$ be the open set based at $S$. Take any $(P,t)\in f^{-1}(U_S)\subseteq X$, for which we will show that there is an open ball $B\owns (P,t)$ completely within $f^{-1}(U_S)$.

Case 1: $t\neq d(P_i,P_j)$ for all pairs $P_i,P_j\in P$. Then set
$$\epsilon = \min\left\{t, \min_{i<j} |t-d(P_i,P_j)|, \min_{i<j} d(P_i,P_j) \right\}.$$ Set $B = B^{\Ran^{\leqslant n}(M)}_{\epsilon/4}(P) \times B^{\R_{>0}}_{\epsilon/4}(t)$, which is an open neighborhood of $(P,t)$ in $X$. It is immediate that $f(P',t')$, for any other $(P',t')\in B$, has all the simplices of $f(P,t)$, as $\epsilon \leqslant |t-d(P_i,P_j)|$ for all $i<j$. If $P_i$ has split in two in $P'$, then for every simplex containing $P_i$ in $f(P,t)$ there are two simplices in $f(P't')$, with either of the points into which $P_i$ split. That is, there may be new simplices in $f(P',t')$, but $f(P',t')$ will be in the image of the splitting maps. Equivalently, $f(P,t)\leqslant f(P',t')$ in $A$, so $B\subseteq f^{-1}(U_S)$.

Case 2: $t= d(P_i,P_j)$ for some pairs $P_i,P_j\in P$. Then set
$$\epsilon = \min\left\{t, \min_{i<j \atop t\neq d(P_i,P_j)} |t-d(P_i,P_j)|,\ \min_{i<j} d(P_i,P_j) \right\},$$ and define $B$ as above. We are using the definition of Vietoris-Rips complex for which we add an edge between $P_i$ and $P_j$ whenever $t>d(P_i,P_j)$. Now take any $(P',t')\in B$ such that its image and the image of $(P,t)$ under $f$ are both in $SC_k/S_k$. Then any points $P_i,P_j \in P$ with $d(P_i,P_j)=t$ that have moved around to get to $P'$, an edge will possibly be added, but never removed, in the image of $f$ (when comparing with the image of $(P,t)$). This means that we have $f(P,t)\leqslant f(P',t')$ in $SC_k/S_k$, so certainly $f(P,t)\leqslant f(P',t')$ in $A$. The same argument as in the first case holds if points of $P$ split. Hence $B\subseteq f^{-1}(U_S)$ in this case as well.  $\square$

This proposition shows in particular that $X$ is poset-stratified by $A$

Perspectives on the Ran space

This post combines the finite subset approach with the mapping space approach of the Ran space, in the context of stratifications. The goal is to understand the colimit construction of the Ran space, as that leads to more powerful results.

Topology

Let $X,Y$ be topological spaces.

Definition: The mapping space of $X$ with respect to $Y$ is the topological space $X^Y = \{f:Y\to X$ continuous$\}$. The topology on $X^Y$ is the compact-open topology which has as basis finite intersections of sets
$$\{f\in X^Y\ :\ f(K)\subseteq U\}, \hspace{3cm} (1)$$
for all $K\subseteq Y$ compact and all $U\subseteq X$ open.

Now fix a positive integer $n$.

Definition: The Ran space of $X$ is the space $\Ran^{\leqslant n}(X) = \{P\subseteq X\ :\ 0<|P|\leqslant n\}$. The topology on $\Ran^{\leqslant n}(X)$ is the coarsest which contains
$$\left\{P\in \Ran^{\leqslant n}(X)\ :\ P\subseteq \bigcup_{i=1}^k U_i,\ P\cap U_i\neq \emptyset\ \forall\ i \right\} \hspace{3cm} (2)$$
as open sets, for all nonempty finite collection of parwise disjoint open sets $\{U_i\}_{i=1}^k$ in $X$.

From now on, we let $I$ be a set of size $n$ and $M$ be a compact, smooth, connected $m$-manifold. There is a natural map
$$\begin{array}{r c l} \varphi\ :\ M^I & \to & \Ran^{\leqslant n}(M), \\ (f:I\to M) & \mapsto & f(I). \end{array}$$
This map is surjective, and for $n>1$, is not injective.

Proposition 1: The map $\varphi$ is continuous and an open map.

Proof: For continuity, take an open set $U\subseteq \Ran^{\leqslant n}(M)$ as in (2) and consider $\varphi^{-1}(U)$. We use the fact that $\{*\}\subset I$ is a compact (in fact open and closed) subset of $I$ and that all the $U_i$ are open, as is their union. Observe that
$$\begin{align*}\varphi^{-1}(U) & = \left\{f\in M^I \ :\ f(I)\subset \bigcup_{i=1}^k U_i,\ f(I)\cap U_i\neq \emptyset\ \forall\ i \right\} \\ & = \left\{f\in M^I\ :\ f(I)\subset \bigcup_{i=1}^k U_i\right\} \cap \bigcap_{i=1}^k \left\{f\in M^I\ :\ f(*\in I) \in U_i\right\},\end{align*}$$
which is a finite intersection of sets of the type (1), and so $\varphi^{-1}(U)$ is open in $M^I$.

For openness, take an open set $V$ as in (1), so $V = \bigcap_{i=1}^k \{f\in M^I\ :\ f(K)\subseteq U_i\}$ for different subsets $K\subseteq I$. By Lemma 1, we may assume that the $U_i$ are pairwise disjoint. For each $U_i$, let $\{U_{i,j}\}_{j=1}^\infty$ be a sequence of increasing open sets in $U_i$ such that $U_{i,j}\subseteq U_{i,j+1}$ and $U_{i,j}\xrightarrow{\ j\to\infty\ } U_i$. Then
$$\varphi (V) = \underbrace{\left\{P\in M\ :\ P\subset \bigcup_{i=1}^k U_i,\ P\cap U_i\neq \emptyset\ \forall\ i\right\}}_{f\in M^I\text{\ with image completely in the\ }U_i} \cup \underbrace{\bigcap_{i=1}^k \bigcup_{j=1}^\infty \left\{ P\in M\ :\ P\subset U_{i,j}\cup \left(\overline{U_{i,j}}\right)^c,\ P\cap U_{i,j}\neq \emptyset,\ P \subset \left(\overline{U_{i,j}}\right)^c \neq \emptyset\right\}}_{f\in M^I\text{\ with image partially in the\ }U_i}.$$
Note that $U_{i,j}$ and $\left(\overline{U_{i,j}}\right)^c$, the complement of the closure of $U_{i,j}$ are both open and disjoint in $M$. Since infinite unions and finite intersections of elements in the topology are also open, we have that $\varphi(V)$ is open in $\Ran^{\leqslant n}(M)$. $\square$

The above proposition says that we may talk equivalently about the compact-open topology on $M^I$ and the Ran space topology on $\Ran^{\leqslant n}(M)$. Viewing the Ran space as a function space allows for more general terminology to be applied.

Lemma 1: Let $U_i\subseteq M$ be open, for $i=1,\dots,k$. Then $\bigcap_{i=1}^k\{f\in M^I\ :\ f(K)\subseteq U_i\}$ may be written as a union of intersections $\bigcap_{j=1}^\ell \{f\in M^I\ :\ f(K)\subseteq V_j\}$ with the $V_j$ open, pairwise disjoint, and $\ell\leqslant k$.

Proof: It suffices to prove this in the case $k=2$. Let $U,V\subseteq M$ open and suppose than $U\cap V\neq \emptyset$. Note that $U\setminus V$ and $V\setminus U$ are separated (that is, $(U\setminus V) \cap \overline{V\setminus U} = \emptyset$ and $(V\setminus U)\cap \overline{U\setminus V} = \emptyset$), and since $\R^N$ is a completely normal space (equivalently, satisfies the $T5$ axiom), there exist disjoint open sets $A,B$ with $U\setminus V\subseteq A$ and $U\setminus V\subseteq B$. So for $A' = A\cap (U\cup V)$ and $B' = B\cap (U\cup V)$, we have
$$\begin{align*} \{f\in M^I\ &:\ f(K)\subseteq U\} \cap \{f\in M^I\ :\ f(K)\subseteq V\} \\ & = \left(\{f\in M^I\ :\ f(K)\subseteq U\setminus V\} \cap \{f\in M^I\ :\ f(K)\subseteq V\setminus U\}\right) \cup \{f\in M^I\ :\ f(K)\subseteq U\cap V \} \\ & = \left(\{f\in M^I\ :\ f(K)\subseteq A'\} \cap \{f\in M^I\ :\ f(K)\subseteq B'\}\right) \cup \{f\in M^I\ :\ f(K)\subseteq U\cap V \}, \end{align*}$$
for $A',B',U\cap V$ open, and $A'\cap B' = \emptyset$.  $\square$

Note that in the last calculation of the proof, the intersection of sets in the second line is smaller than the intersection of sets in the last line (as $U\setminus V \subsetneq A$ and $V\setminus U\subsetneq B$). However, all the extra ones in the third line appear in the set $\{f\in M^I\ :\ f(K)\subseteq U\cap V\}$.

Stratifications

Now we compare stratifications on $M^I$ and $\Ran^{\leqslant n}(M)$. As before, $I$ is a set of size $n$.

Corollary: An image-constant $A$-stratification on $M^I$ is equivalent to an $A$-stratification on $\Ran^{\leqslant n}(M)$.

This follows from Proposition 1. By image-constant we mean if $\alpha,\beta\in M^I$ have the same image (that is, $\alpha(I)=\beta(I)$), then $\alpha,\beta$ are sent to the same element of $A$.

Proof: If we start with a continuous map $f:M^I\to A$, setting $g(P) = f(I\to M)$ whenever $(I\to M) \in \varphi^{-1}(P)$ is continuous, as $\varphi(f^{-1}(U))$ is open, by continuity of $f$ and openness of $\varphi$. The assignment $g(P) = f(I\to M)$ whenever $(I\to M) \in \varphi^{-1}(P)$ is well defined, as the stratification is image-constant, so any continuous map from $M^I$ must send every element of $\varphi^{-1}(P)$ to the same place.

Conversely, if we start with a continuous map $g:\Ran^{\leqslant n}(M)\to A$, setting $f(I\to M) = g(\varphi(I\to M))$ is continuous, as $\varphi^{-1}(g^{-1}(U))$ is open, by continuity of $g$ and continuity of $\varphi$. This map is image-constant, as $\varphi(\alpha:I\to M) = \alpha(I)$. $\square$

Next we consider a particular stratification of $M^I$, adapted from Example 3.5.17 of Ayala-Francis-Tanaka, simplified with $P=\{*\}$. That is, the example begins with a stratified space $M\to P$ and proceeds to construct another stratification $M^I\to P'$, but we only consider the trivial stratification $M\to \{*\}$.

Definition: Given $M$ and $I$, let the poset $\mathcal P(I)$ of coincidences on $I$ be the set of equivalence relations on $I$, ordered by reverse set inclusion. Let $f_I:M^I\to \mathcal P(I)$ be the natural stratification that takes a map $\alpha: I\to M$ to the equivalence relation on $I$ describing which elements of $I$ coincide in the image of $\alpha$.

Example: An element of $\mathcal P(I)$ is a subset of $I\times I$ always containing $(a,a)$ for every $a\in I$ (reflexivity), and satisfying the symmetry and transitivity conditions. For example, if $|I|=3$ or 4, then $\mathcal P(I)$ is ordered as in the diagrams below, with order increasing from left to right. We simplify things by writing $[x_1,\dots,x_k]$ for the collection $(x_i,x_j)$ of all $i\neq j$ (the equivalence class).

To check that the map $f_I:M^I\to \mathcal P(I)$ is continuous, we first note that an element $U_{[x_1],\dots,[x_k]}$ in the basis of the upwards-directed topology on $\mathcal P(I)$ contains images of $\alpha\in M^I$ whose images have at most the elements of each equivalence class $[x_i]$ coinciding. Hence
$$f_I^{-1}(U_{[x_1],\dots,[x_k]}) = \bigcup_{U_1,\dots,U_k\subseteq M \atop \text{open, disjoint}}\ \bigcap_{i=1}^k \left\{\alpha\in M^I\ :\ \alpha(K = \{x\in [x_i]\}) \subseteq U_i\right\},$$
which is an open set in the compact-open topolgy on $M^I$.

The Ran space as a colimit

Beilinson-Drinfeld (Section 3.4) and Ayala-Francis-Tanaka (Section 3.7) describe the Ran space as a colimit, the former of a functor into topological spaces, the latter of a functor into stratified spaces. See Mac Lane for a full treatment of colimits. Both BD and AFT use the category $\Fin^{surj,\leqslant n}$ of finite sets and surjections, that is,
$$\begin{align*}\Obj(\Fin^{surj,\leqslant n}) & = \{I\in \Obj(\Set)\ :\ 0<|I|\leqslant n\}, \\ \Hom_{\Fin^{surj,\leqslant n}}(I,J) & = \begin{cases} \emptyset, & \text{\ if\ } |I|<|J|, \\ \left\{\text{surjections\ }I\to J\right\}, & \text{\ if\ } |I|\geqslant |J|. \end{cases}\end{align*}$$
AFT uses more involved terminology, with "conically smooth" stratified spaces instead of just poset-stratified. They use a category $\Strat$, which for our purposes we may define as
$$\begin{align*} \Obj(\Strat) & = \{\text{poset-stratified topological spaces }X\xrightarrow{ f } A\}, \\ \Hom_{\Strat}(X\xrightarrow{ f } A,Y\xrightarrow{ g } B) & = \{(\mu\in \Hom_{\Top}(X,Y), \nu \in \Hom_{\Set}(A,B)\ :\ g\circ \mu = \nu\circ f\}. \end{align*}$$

Remark:  There is a natural functor $\mathcal F_M:(\Fin^{surj,\leqslant n})^{op} \to \Top$, given by $I\mapsto M^I$. A surjection $s:I\to J$ induces a map $M^J\to M^I$, with $(f:J\to M)\mapsto (f\circ s :I\to M)$. BD use this to declare that $\Ran^{\leqslant n}(M) = \colim(\mathcal F_M)$.

Remark: There is also a natural functor $\mathcal G_M:(\Fin^{surj,\leqslant n})^{op} \to \Strat$, given by $I\mapsto (M^I\to \mathcal P(I))$. AFT use this to declare that $(\Ran^{\leqslant n}(M)\to \{1,\dots,n\}) = \colim(\mathcal G_M)$.

The construction of AFT is even more general, as they consider the Ran space of an already stratified space. Here we use their result for $M\to \{*\}$ trivially stratified.

References: Ayala, Francis, and Tanaka (Local structures on stratified spaces, Sections 3.5 and 3.7), Beilinson and Drinfeld (Chiral algebras, Section 3.4), Mac Lane (Categories for the working mathematician, Chapter III.3)

Towards a sheaf of simplicial complexes

The goal of this post is to describe a new stratification of $\Ran^n(M)\times \R_{\geqslant 0}$ that builds on the ideas from a previous post (see "The point-counting stratification of the Ran space is conical (really though) ," 2017-11-15) and some newer ones.

Let $SC_n$ be the set of simplicial complexes on $n$ ordered vertices. There is a natural partial order on $SC_n$ given by inclusion of sets, viewing every simplex as a subset of the power set $\mathbf P(\{1,\dots,n\})$. The symmetric group $S_n$ has a natural action on $SC_n$ and $SC_n/S_n$ has an induced partial order as well. Hence we have a map
$$\begin{array}{r c l} f\ :\ \Ran^n(M)\times \R_{\geqslant 0} & \to & SC_n/S_n, \\ (P,t) & \mapsto & VR(P,t), \end{array}$$
where $VR(P,t)$ is the Vietoris-Rips complex on $P$ with radius $t$. We include a $k$-cell in $VR(P,t)$ at the vertices $\{P_0,\dots,P_k\}\subset P$ if $d(P_i,P_j)<t$ for all $0\leqslant i<j\leqslant k$. Because we have strict inequality, the map is continuous in the upwards-directed, or Alexandrov topology on $SC_n/S_n$. Indeed, taking the preimage of an open set $U_S$ in $SC_n/S_n$ based at some simplicial complex $S$ (such $U_S$ form the basis of topology on $SC_n/S_n$), there is an open ball of radius $\min_{i<j} d(P_i,P_j)/2$ in the $\Ran^n(M)$ component and $\min_{(P_i,P_j)\subset f(P,t)} |t-d(P_i,P_j)|$ in the $\R_{\geqslant 0}$ component around any $(P,t)\in f^{-1}(U_S)$.

Remark: The above shows that $\Ran^n(M)\times \R_{\geqslant 0}$ is poset-stratified by $SC_n/S_n$, in the sense of Definition A.5.1 of Lurie. However, the strata are all of the same dimension, so there is no chance of this being a conical stratification, in the sense of Definition A.5.5 of Lurie. We hope to fix that with a different stratification.

Definition: Construct a poset $(A,\leqslant_A)$ in the following way:

• $SC_n/S_n \subset A$, with $S\leqslant_A T$ whenever $S\leqslant_{SC_n/S_n} T$ ,
• for every $S\neq T\in SC_n/S_n$, let $a_{ST}\in A$ with $a_{ST}\leqslant_A S$ and $a_{ST}\leqslant_A T$,
• for every $\{S_1,\dots,S_{k>2}\}\subset SC_n/S_n$, let $a_{S_1\cdots S_k}\in A$ with $a_{S_1\cdots S_k} \leqslant_A a_{S_1\cdots \widehat{S_i}\cdots S_k}$ for all $1\leqslant i\leqslant k$.

Define a map into $(A,\leqslant_A)$ in the following way:
$$\begin{array}{r c l} g\ :\ \Ran^n(M)\times \R_{\geqslant 0} & \to & A, \\ (P,t) & \mapsto & \begin{cases} S, & \text{ if $(P,t)\in \text{int}(f^{-1}(S))$ for some }S\in SC_n/S_n, \\ a_{S_1\cdots S_k}, & \text{ if }(P,t)\in \text{cl}(f^{-1}(T))\ \iff\ T\in \{S_1,\dots,S_k\}. \end{cases} \end{array}$$

We now claim that $g$ is a stratifying map.

Proposition: The map $g$ is continuous.

Proof: Since $\text{int}(f^{-1}(S))\cap \text{int}(f^{-1}(T)) = \emptyset$ for all $S\neq T\in SC_n/S_n$, the open sets $U_S\subseteq A$ based at $S$ all have open preimage $g^{-1}(U_S) \subseteq X$. Now take $(P,t)\in g^{-1}(U_{a_{S_1\cdots S_k}})$, for $k\geqslant 2$. If every open ball around $(P,t)\in X$ intersects $X_{a_{\mathbf T}}$, for some $\mathbf T \subseteq SC_n/S_n$, then $(P,t)$ must be in the closure of $f^{-1}(T)$, for every $T\in \mathbf T$. Hence the only possible such $\mathbf T$ are $\mathbf T\subseteq \{S_1,\dots,S_k\}$, so $g^{-1}(U_{a_{S_1\cdots S_k}})$ is open in $X$. $\square$

The next step would be to show that this stratification is conical, though it is not clear yet if it is.

References: Lurie (Higher Algebra, Appendix A)

The point-counting stratification of the Ran space is conical (really though)

This post is meant to correct the issues of a previous post ("The point-counting stratification of the Ran space is conical," 2017-11-06). The setting is the same as before.

A key object here will be the Ran space of a disconnected space. If $M$ has $k$ connected components, then $\Ran^{\leq n}(M)$, for $k\leq n$, has $2^k$ connected components (as we must choose whether or not to have at least one point in each component). When $M$ is disconnected with $k\leq n$ components, let $\Ran^{\leq n}(M)'$ be the largest connected component of $\Ran^{\leq n}(M)$, that is, the one with at least one point in every component of $M$.

Proposition 1: The point-counting stratification $f:X\to A$ is conical.

Proof: Fix $P=\{P_1,\dots,P_k\}\in \Ran^k(M)\subseteq \Ran^{\leqslant n}(M)$ and set $2\epsilon = \min_{i<j}d(P_i,P_j)$. Set
$$Z := \prod_{i=1}^k B^{\R^m}_{\epsilon/3}(0), \hspace{.5cm} Y := \Bigg\{(Q^1,\dots,Q^k)\in \underbrace{\Ran^{\leq n}\left(\coprod_{i=1}^k B^{\R^m}_{2\epsilon/3}(0)\right)'}_{W}\ :\ \overbrace{\sum_{i=1}^k \mathbf d(\{0\},Q^i)=\frac{2\epsilon}3}^{\text{the cone condition}}\ ,\ \hspace{-5pt}\underbrace{\sum_{j=1}^{|Q^i|}Q_j^i =0}_{\text{the centroid condition}}\hspace{-5pt}\ \forall\ i\Bigg\}.$$
The cone condition ensures the right topology at the cone point of $C(Y)$. The centroid condition ensures injectivity of $\varphi_P$ when multiplying by $Z$. Reasoning for the constants $\epsilon/3$ and $2\epsilon/3$ is given in Proposition 2. The balls $B_{\epsilon/3}$ in $Z$ are open and the balls $B_{2\epsilon/3}$ in $Y$ are closed. The collection $Q^i$ is all the points in the $i$th ball $B_{2\epsilon/3}$. The product $Z\times C(Y)$ is given the topology for which a set $U$ is open if $\varphi_P(U)$ is open in the subspace topology on $\im(\varphi_P)\subseteq X$.

If $k=n$, then $Y=\emptyset$ because of the cone and centroid conditions. Then $C(Y)=*$ and $Z\times * \cong Z$ is by construction an open set in $X$, so $X$ is conically stratified at $P$. If $k<n$, then $Y$ has a natural $A_{>k}$ stratification $$(Q^1,\dots,Q^k) \mapsto \sum_{i=1}^k |Q^i| \in \{k+1,\dots,n\},$$
with the image landing in $A_{>k}=\{k+1,\dots,n\}$ because there are at least $k$ points in every element of $W$, and to satisfy the cone condition at least one $Q^i$ must have at least two points. We now claim that
$$\begin{array}{r c l} \varphi_P\ :\ Z \times C(Y) & \to & X, \\ (R,(Q^1,\dots,Q^k),t\neq 0) & \mapsto & \{P_1+R_1+tQ^1,\dots,P_k+R_k+tQ^k\},\\ (R,*,0) & \mapsto & \{P_1+R_1,\dots,P_k+R_k\} \end{array}$$
is an open embedding. Here $t\in [0,1)$ is the cone component and $P_i+R_i+Q^i$ is the collection of all $P_i+R_i+Q^i_j,$ for $j=1,\dots,|Q^i|$. Injectivity follows from the cone condition and centroid condition on $Y$: it is clear that for fixed $R\in Z$ the map $\varphi_P$ is injective, as we are taking points at different distances from $P_i+R_i$ (the cone condition). Because of the centroid condition, moving around to different $R$ means the centroid will also move, so we will not get a collection of points we previously had.

Further, $Z\times C(Y)$ gets mapped homeomorphically into $X$ because of the topology forced upon it - continuity and openness of the map follow immediately. Finally, since $\im(\varphi_P)$ is open in $X$, $\varphi_P$ is an open embedding, so $X$ is conically stratified at $P$. $\square$

The following proposition gives a better idea of where $\im(\varphi_P)$ actually lands in $X$.

Proposition 2: For $\varphi_P$ as above, we have $B^X_{2\epsilon/3k}(P)\subseteq \im(\varphi_P)\subseteq B^X_{\epsilon}(P)$.

Proof: For the first inclusion, take $S\in B^X_{2\epsilon/3k}(P)$ and for every $1\leq i\leq k$ set
$$\begin{align*}S^i & := \{s\in S\ :\ d(s,P_i)<d(s,P_j)\ \forall\ j\neq i\}, & (\text{points closest to $P_i$}) \\ T_i & := \frac1{|S^i|}\sum_{j=1}^{|S^i|} S^i_j, & (\text{centroid of the $S^i_j$}) \\ c_i & := \mathbf d(\{T_i\},S^i). & (\text{distance from the $S^i_j$ to their centroid})\end{align*}$$
If $|S|=k$, then $c_i=0$ for all $i$, and $t=0$, so we are at the cone point, and $S = \varphi_P(T-P,*,0)$. If $|S|>k$, then $0<\sum_i c_i <2\epsilon/3$, as $c_i < 2\epsilon/{3k}$ for all $i$, so there is some $t'\in (0,1)$ such that $\sum_i c_i = t'2\epsilon/3$. Then
$$\begin{align*}\varphi_P\left(T-P, \left( {\textstyle \frac1{t'}} (S^1-T_1),\dots, {\textstyle \frac1{t'}}(S^k-T_k) \right), t'\right) & = \left\{ P_1+(T-P)_1 + t'{\textstyle \frac1{t'}}(S^1-T_1), \dots, P_k+(T-P)_k + t'{\textstyle \frac1{t'}}(S^k-T_k)\right\} \\ & = \left\{ P_1+T_1-P_1 + S^1-T_1, \dots, P_k+T_k-P_k + S^k-T_k\right\} \\ & = \left\{S^1, \dots, S^k\right\} \\ & = S.\end{align*}$$
Note that since $T_i$ is the centroid of the $S^i_j$, and $S^i \subset B^M_{2\epsilon/3k}(P_i)$, and the centroid of a collection of points is in their convex hull, we also have $T_i\in B^M_{2\epsilon/3k}(P_i)$. Since $\frac{2\epsilon}{3k}<\frac{\epsilon}3$ when $k>2$, we have that $P_i-T_i\in B^{\R^m}_{\epsilon/3}(0)$. If $k\leq 2$, then use $k+2$ instead of $k$. Finally, since $\sum_i c_i/t' = 2\epsilon/3$ and $c_i,t\geq 0$, we have that $c_i/t'\leq 2\epsilon/3$, meaning that $\frac1{t'}(S^i-T_i)\subset B^{\R^m}_{2\epsilon/3}(0)$. Hence the argument of $\varphi_P$ given above is in the domain of $\varphi_P$.

For the second inclusion, first fix $i$. For an element in the image of $\varphi_P$, note that $d(P_i,P_i+R_i)\leqslant \epsilon/3$ and $\mathbf d(\{R_i\},tQ^i)<\mathbf d(\{R_i\},Q^i)\leq 2\epsilon/3$. Since $d(P_i,R_i) = \mathbf d(\{P_i\},\{R_i\})$, we have that
$$\begin{align*}\mathbf d(\{P_i\},P_i+R_i+tQ^i) & \leqslant \mathbf d(\{P_i\},\{P_i+R_i\})+\mathbf d(\{P_i+R_i\},P_i+R_i+tQ^i) & (\text{triangle inequality}) \\ & = \mathbf d(\{0\},\{R_i\}) + \mathbf d(\{0\},tQ^i) & (\text{linearity of $\mathbf d$}) \\ & = \mathbf d(\{0\},\{R_i\}) + t\mathbf d(\{0\},Q^i) & (\text{linearity of $\mathbf d$}) \\ & < \frac{\epsilon}3 +\frac{2\epsilon}3 & (\text{assumption}) \\ & = \epsilon.\end{align*}$$ $\square$

The following diagram describes the last calculation in the proof.

The point-counting stratification of the Ran space is conical

Note: There are problems with the proof here, in particular with making the map $\varphi$ an embedding. The mistakes are corrected in a later post ("The point-counting stratification of the Ran space is conical (really though)," 2017-11-15).

---

This post completes the effort of several previous posts to show that $f:\Ran^{\leqslant n}(M)\to A=\{1,\dots,n\}$ is a conically stratified space, where $f$ is the point-counting map, for $M$ a compact smooth $m$-manifold embedded in $\R^N$.

Remark: Since $M$ is a manifold, we will work on $M$ or through charts in $\R^m$, as necessary, without explicitly mentioning the charts or domains. Balls $B^M_\lambda, B^{\R^m}_\lambda$ of radius $\lambda$ will be closed and $\mathcal B^{\R^m}_\lambda,\mathcal B^X_\lambda$ will be open. We write $d$ for distance between points of $M$ (or $\R^m$) and $\mathbf d$ for distance between finite subsets of $\R^m$. This is essentially the definition given by Remark 5.5.1.5 of Lurie: $$\mathbf d(P,Q) = \frac 12 \left(\sup_{p\in P}\inf_{q\in Q} d(p,q) + \sup_{q\in Q}\inf_{p\in P}d(p,q)\right).$$ We add the $\frac 12$ so that $\mathbf d(\{p\},\{q\}) = d(p,q)$. Note also $\sup,\inf$ may be replaced by $\max,\min$ in the finite case.

Remark: In our context, given $P\in X$, $\mathbf d$ may be thought of as how far away have new points split off from the $P_i$. That is, if $Q\in X$ is close to $P$ representing the $P_i$ splitting up, then $\mathbf d(P,Q)$ is (half) the sum of the distance to the farthest point splitting off from the $P_i$ and to the farthest point among every $P_i$'s closest point. The diagram below gives the idea.

Then the distance between $P$ and $Q$ is given by
$$\begin{align*} \mathbf d(P,Q) & = \frac12 \left(\sup_{P_i}\left\{\inf_{Q_j}\left\{d(P_i,Q_j)\right\}\right\} + \sup_{Q_j}\left\{\inf_{P_i}\left\{d(P_i,Q_j)\right\}\right\}\right) \\ & = \frac12\left(\sup \left\{\inf\left\{a,b,c\right\}, \inf\left\{d,e,f,g\right\}\right\} + \sup \left\{ a,b,c,d,e,f,g \right\}\right) \\ & = \frac12\left( \sup\left\{ a,g \right\} + c \right) \\ & = \frac12(a+c). \end{align*}$$

Now we move on to the main result.

Proposition: The point-counting stratification $f:X\to A$ is conical.

Proof: Fix $P=\{P_1,\dots,P_k\}\in \Ran^k(M)\subseteq \Ran^{\leqslant n}(M)$ and set $2\epsilon = \min_{i<j}d(P_i,P_j)$. Set $$Z = \prod_{i=1}^k \mathcal B^{\R^m}_\epsilon(0), \hspace{2cm} Y = \coprod_{\sum \ell_i=n \atop \sum t_i = \epsilon} \prod_{i=1}^k\ \left\{Q\in \Ran^{\ell_i}(B^{\R^m}_{t_i}(0))\ :\ \textbf d(0,Q) = t_i,\ \textstyle \sum Q_j = 0 \right\},$$ both of which are topological spaces. The first condition on elements of $Y$ is the cone condition, which ensures the right topology at the cone point in $C(Y)$. The second condition on $Y$ is the centroid condition, which ensures that the point to which 0 maps to (under $\varphi$) is the centroid of points splitting off it, so that we don't overcount when multiplying by $Z$. For $C(Y) = (Y\times [0,1))/(Y\times \{0\})$ the cone of $Y$, define a map $$\begin{array}{r c l} \varphi\ :\ C(Y)\times Z & \to & X, \\ \left(\Ran^{\ell_i}(B_{t_i}^{\R^m}(0)),t,R\right) & \mapsto & \Ran^{\ell_i}(B_{tt_i}^M(R_i)), \end{array}$$ where $t\in [0,1)$ is the cone component and $R=\{R_1,\dots,R_k\}\in Z$ is an element of $\Ran^k(M)$ near $P$. It is sufficient to describe where the $\Ran^{\ell_i}$ map to, as all the $Q$ in a fixed $\Ran^{\ell_i}$ map in the same way into $X$.

The map $\varphi$ is continuous by construction, injective by the centroid condition, and a homeomorphism onto its image by the cone condition. Hence $\varphi$ is an embedding, and since the image is open, it is an open embedding. Note that we are taking "open embedding" to mean an embedding whose image is open. Hence every $P\in X$ satisfies Definition A.5.5 of Lurie, so $f:X\to A$ is conically stratified.  $\square$

Remark: Observe that $\mathcal B^X_{\epsilon/k}(P)\subseteq \im(\varphi) \subseteq \mathcal B^X_\epsilon(P)$, both inclusions coming from the $\sum t_i=\epsilon$ condition.

Combined with the proposition of a previous post ("Splitting points in two," 2017-11-02) and Theorem A.9.3 of Lurie, it follows that $A$-constructible sheaves on $X$ are equivalent to functors of $A$-exit paths on $X$ to the category $\mathcal S$ of spaces. A previously given construction (in "Exit paths, part 2," 2017-09-28) gives such a functor, indicating that there exists an $A$-constructible sheaf on $X$.

Next steps may involve applying this approach to the space $\Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$, which was the motivator for all this, or continuing with Lurie's work to see how far this can be taken.

References: Lurie (Higher Algebra, Appendix A), nLab (article "Embedding of topological spaces")

Splitting points in two

The goal of this post is to expand upon some final ideas in a previous post ("Atempts at proving conical stratification," 2017-10-27). Let $M$ be a compact smooth $m$-manifold embedded in $\R^N$, and fix $n\in \Z_{>0}$. Let $X = \Ran^{\leqslant n}(M)$ and $f:X\to A=\{1,\dots,n\}$ the usual point-counting stratification. Let $$\begin{align*} B^X_\epsilon(P) & = \left\{Q\in X\ :\ 2d_M(P,Q) =\sup_{p\in P}\inf_{q\in Q} d_M(p,q) + \sup_{q\in Q}\inf_{p\in P}d_M(p,q) < 2\epsilon\right\}, \\ B^M_\epsilon(p) & = \left\{q\in M\ :\ d_M(p,q) <\epsilon\right\},\\ B^{\R^m}_\epsilon(0) & = \left\{x\in \R^m\ :\ d(0,x)<\epsilon\right\} \end{align*}$$ be open balls in their respective spaces. We use $d_M$ for distance on $M$ and $d$ for distance in $\R^N$. Since $M$ is an $m$-manifold, we will work in charts in $\R^m$ when necessary.

Proposition: The stratification $f:X\to A$ is conical in the top two strata $\Ran^n(M)$ and $\Ran^{n-1}(M)$.

Proof: Let $P = \{P_1,\dots,P_n\}\in \Ran^n(M)$ and $2\epsilon = \min_{1\leqslant i <j\leqslant n}d(P_i,P_j)$. Let $Y = \emptyset$ which has a natural $(A_{>n} = \emptyset)$-stratification with $C(Y) = \{*\}$ having a natural $(A_{\geqslant n} = \{n\})$-stratification. Let $Z = B^X_\epsilon(P) = \prod_{i=1}^nB^M_\epsilon(P_i)$, for which the identity map $Z\times \{*\} \cong Z\hookrightarrow X$ is an open embedding. Hence $X$ is stratified at every $P\in \Ran^n(M)$.

Let $P = \{P_1,\dots,P_{n-1}\}\in \Ran^{n-1}(M)$ and $2\epsilon = \min_{1\leqslant i <j\leqslant n-1}d(P_i,P_j)$. Let $$Y = \coprod_{i=1}^{n-1} \mathbf P\partial B^{\R^m}_{\epsilon/2}(0), \hspace{1cm} Z = B^{\R^m}_{\epsilon/2}(0),$$ where $\mathbf P\partial B$ is the projectivization of the sphere, so may be viewed as a collection of unique pairs $\{\vec v, -\vec v\}$. Then the cone $C(Y)$ may be viewed as a collection of pairs $\{\vec v,t>0\}$ along with the singleton $\{0\}$, with the usual cone topology. Define a map $$\begin{array}{r c l} \varphi\ :\ Z\times C(Y) & \to & X, \\ (x,\vec v,t) & \mapsto & \{x+t\vec v,x-t\vec v\} ,\\ (x,0) & \mapsto & \{x\}. \end{array}$$ Note that $B^X_{\epsilon/2}(P) \subseteq \im(\varphi)\subseteq B^X_\epsilon(P)$. This map is injective as every pair of points on $M$ within an $\epsilon/2$-radius of $P_i$ is uniquely defined by their midpoint (the element of $Z$), a direction from that midpoint (the element of $Y$) and a distance from that midpoint (the cone component $t\in [0,1)$). By construction $\varphi$ is continuous and an embedding. The map takes open sets to open sets, so we have an open embedding into $X$. Hence $X$ is conically stratified at every $P\in \Ran^{n-1}(M)$. $\square$

The problem with generalizing this to $P\in \Ran^k(M)$ for all other $k$ is that an $(n-k+1)$-tuple of points has no unique midpoint. It does have a unique centroid, but it is not clear what the $[0,1)$ component of the cone should then be.

Proposition: The space $X$ is of locally singular shape.

Proof: First note that every $P\in X$ has an open neighborhood that is homemorphic to an open ball of dimension $mn$ (see Equation (1) of previous post "Attempts at proving conical stratification," 2017-10-27). Hence we may cover $X$ by contractible sets. By Remark A.4.16 of Lurie, $X$ will be of locally singular shape if every element of the cover is of singular shape. Since all elements of the cover are contractible, by Remark A.4.11 of Lurie we only need to check if the topological space $*$ is of singular shape. Finally, Example A.4.12 of Lurie gives that $*$ has singular shape. $\square$

References: Lurie (Higher algebra, Appendix A)

Attempts at proving conical stratification

This post chronicles several attempts and failures to show that $X=\Ran^{\leqslant n}(M)$ is conically stratified. Here $M$ will be a smooth, compact manifold of dimension $m$, embedded in $\R^N$ for $N\gg 0$. Recall that a stratified space $f:X\to A$ is conically stratitifed at $x\in X$ if there exist:

1. a stratified space $g:Y\to A_{>f(x)}$,
2. a topological space $Z$, and
3. an open embedding $Z\times C(Y)\hookrightarrow X$ of stratified spaces whose image contains $x$.

The cone $C(Y)$ has a natural stratification $g':C(Y)\to A_{\geqslant f(x)}$, as does the product $Z\times C(Y)$. The space $X$ itself is conically stratified if it is conically stratfied at every $x\in X$.

Let $P=\{P_1,\dots,P_k\}\in \Ran^k(M)\subseteq \Ran^{\leqslant n}(M)=X$, and $2\epsilon = \min_{1\leqslant i<j\leqslant k}\{d(P_i,P_j)\}$.

Observations

Observation 1: When $M=I = (0,1)$, the interval, we can visualize what $\Ran^{\leqslant 3}(M)$ looks like via the construction $\Ran^{\leqslant 3}(M) = (M^3\setminus \Delta_3)/ S_3$, to gain some intuition about what the Ran space looks like in general. 

A drawback is that $\dim(M)=1$, which masks the problems in higher dimensions.

Observation 2: An open neighborhood of $P\in X$ looks like
$$\coprod_{\sum \ell_i = n \atop \ell_i\in \Z_{>0}}\ \prod_{i=1}^k \Ran^{\leqslant \ell_i}(B^M_\epsilon(P_i)) = B^X_{\epsilon/2}(P) \times \coprod_{\sum \ell_i = n \atop \ell_i\in \Z_{>0}}\ \prod_{i=1}^k \Ran^{\leqslant \ell_i}(B^M_{\epsilon/2}(P_i)),\hspace{2cm} (1)$$
for $B^M_\epsilon(x) = \{y\in M\ :\ d_M(x,y)<\epsilon\}$ the open ball of radius $\epsilon$ around $x\in M$, and similarly for $P\in X$. Most attempts to prove conical stratification are based around expressing these as $Z\times C(Y)$, usually for $Z=B_{\epsilon/2}^X(P)$.

Observation 3: When $k<n$, the "steepest" direction from $P_i$ into the highest stratum of $X$ is given by $P_i$ splitting into $n-k+1$ points uniformly distributed on $\partial B^M_t(P_i)$. Hence the $[0,1)$ part of the cone (recall $C(Y)=Y\times [0,1)/\sim$) should be along $t\in [0,1)$.

Attempts

Attempt 1: Use more resrictive (but better described) AFT definition.

Ayala-Francis-Tanaka describe $C^0$ stratified spaces, a special type of stratified space. Any space that has a cover by topological manifolds is a $C^0$ stratified space, however it seems that $X$ cannot be covered by topological manifolds. Even further, each element in the cover must have the trivial stratification, and since we must have overlaps, $f:X\to A$ will have $A=\{*\}$, which is not what we want.

Attempt 2: Stratify $\Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$ instead.

This is more difficult, but was the original impetus, with strata defined by collecting the Vietoris-Rips complexes $VR(P,t)$ of the same type. The problem is that this space has strata next to each other of the same dimension, which does not conform to a standard definition of stratification, and so doesn't admit a conical stratification. Dimension counting and requiring an open embedding $Z\times C(Y)\hookrightarrow X$ shows this is impossible at the boundary point between two such strata.

Weinberger gives some standard stratifed space types, among them a manifold stratified space, a manifold stratified space with boundary, and a PL stratified space, but $X\times \R_{\geqslant 0}$ is none of these.

Attempt 3: Naively describe the neighborhood of $P$ as a cone. 

This is the most direct attempt to write (1) as $Z\times C(Y)$. If we say
$$C(Y) = \underbrace{\coprod_{\sum \ell_i = n \atop \ell_i\in \Z_{>0}}\ \prod_{i=1}^k \Ran^{\leqslant \ell_i}(\partial B^M_{t}(P_i))}_{Y} \times [0,\epsilon/2) \Bigg/\sim,$$
then we miss points splitting off at different "speeds". That is, in this presentation $P_i$ can only split into points that are all the same distance away from it. Between such a collection of points and $P_i$ are points that are some closer, some the same distance away, and those are not accounted for.

Moreover, using $Z=B^X_{\epsilon/2}(P)$, leads to overcounting, and the map into $X$ would not be injective.

Attempt 4: Iterate over different number of points at common radius.

This came out of an attempt to fix the previous attempt. As in a previous post ("The Ran space is locally conical," 2017-10-22), let $E_\ell$ be the collection of distinct partitions of $\ell$ elements, and for $e\in E_\ell$, let $T(e)$ be the collection of distinct total orderings of $e$. A candidate for $Z\times C(Y)$ would then be

with $t_{i,0} = \epsilon$ and $t_{i,j>0}$ the chosen element of $(0,t_{i,j-1})$. The open embedding $Z\times C(Y) \to X$ would be the inclusion on the $C(Y)$ component, and would scale every factor in the $Z$ component to a neighborhood of $P_i$ of radius $t_{i,|\tau_i|}$. However, this embedding is not continuous, because a point in $\Ran^k(M)$ is next to a point in $\Ran^{n}(M)$, where $P_i$ has split off into $n-k$ points, but the radius of $B^M_\epsilon(P_i)$ in $\Ran^k(M)$ is $\epsilon$, while in $\Ran^n(M)$ it is the shortest distance from one of the new points to $P_i$.

Attempt 5: Iterate over common radii, but only "antipodal" points.
This was an attempt to fix the previous attempt and combine it with the naive description. In fact, this approach works when $k=1$ and $n=2$. Then $P = \{P_1\}$, and
$$B^M_\epsilon(P_1) \times \left.\left(\mathbf P\partial B^M_t(P_1) \times [0,1)\right)\right/\sim$$
maps into $B^X_\epsilon(P_1)$ by first scaling $[0,1)$ down to $[0,\epsilon-d_M(P,P_1))$, where $P\in B^M_\epsilon(P_1)$ is the chosen point. The object $\mathbf P\partial B^M_t(P_1)$ is the projectivization of the boundary of the open $\dim(M)$-ball of radius $t$ around $P_1$ on $M$. That is, every element in it is a pair of antipodal points on the boundary of this ball that are exactly $t\in [0,\epsilon-d_M(P,P_1))$ away from $P_1$.

This works because every pair of points in a contractible neighborhood of $P_1$ is described uniquely by a pair $(P,v)$, for $P$ the midpoint of the two points and $v$ the $\dim(M)$-vector giving the direction of the points from $P$ (this may rely on working in charts, which is fine, as $M$ is a manifold). However, trying to generalize to more than two points fails because $\ell>2$ points in general are not equally distributed on a sphere. If instead of using the "antipodal" property we take a point from which all $\ell$ points are equidistant, this point may not be in the $\epsilon$-neighborhood of $P_1$.

Possible solutions

Solution 1: Instead of a smooth manifold, let $M$ be a simplicial complex. Then $\Ran^{\leqslant n}(M)$ should also be a simplicial complex. Then it may be possible to apply a general theorem to find appropriate cones.

Solution 2: Extend the only partially successful attempt, Attempt 5. Extend by describing a point splitting off into $\ell$ pieces as a sequence of points splitting into 2 pieces. Or, extend by using the centroid of $\ell$ points instead of the midpoint.

Solution 3: Weaken definition of "conically stratifed" to exclude either open embedding condition or $A_{>f(x)}$ stratification of $Y$, though this would involve following out Lurie's proof to see what can not be concluded.

References: Lurie (Higher algebra, Appendix A), Ayala, Francis and Tanaka (Local structures on stratified spaces, Sections 2 and 3), Weinberger (The classification of topologically stratified spaces)

The Ran space is locally conical

In this post we show that every point in the Ran space $\Ran^{\leqslant n}(M)$, for $M$ a compact, smooth embedded manifold, is the base of a cone in $\Ran^{\leqslant n}(M)$. Let $\dim(M) = m$ and let $P=\{P_1,\dots,P_k\}\in \Ran^k(M)\subseteq \Ran^{\leqslant n}(M)$. We write $d(x,y)$ for distance in Euclidean space $\R^N$ where $M$ is embedded, and $d_M(x,y)$ for distance on the embedded manifold $M$ (note $d\leqslant d_M$). Define the following objects:
$$\begin{align*} N_\epsilon(x) & = \{z\in M\ :\ d_M(x,z)<\epsilon\}, \\ E_n & = \{\text{distinct partitions of an unlabeled set of $n$ elements}\}, \\ T(e) & = \{\text{distinct total orderings of }e\in E_n\}. \end{align*}$$
We write $\tau=(\tau_1<\cdots<\tau_{|\tau|})$ for an element $\tau\in T(e)$.

Example: Let $n=4$, so then
$$E_4 = \Big\{\{\{*\},\{*\},\{*\},\{*\}\},\hspace{10pt} \{\{*,*\},\{*\},\{*\}\},\hspace{10pt} \{\{*,*\},\{*,*\}\},\hspace{10pt} \{\{*,*,*\},\{*\}\},\hspace{10pt} \{\{*,*,*,*\}\}\Big\}.$$
By stacking the $*$ on top of one another to indicate containment in a single set, and for order increasing from left to right, we have the following distinct total orderings for every element of $E_4$.

Set $\epsilon = \min_{1\leqslant i<j\leqslant k}\{d(P_i,P_j)\}$, $t_0\in(0,\epsilon/2)$, and $t_{j>0}\in (0,t_{j-1})$. By construction, the object
$$\begin{align*} C_P & = \{P\} \cup \coprod_{\genfrac{}{}{0pt}{}{\sum \ell_i=n-k}{\ell_i \in \Z_{>0}}}\ \prod_{i=1}^k\  \coprod_{\genfrac{}{}{0pt}{}{\tau\in T(e)}{e\in E_{\ell_i}}}\  \prod_{j=1}^{|\tau|} \Ran^{|\tau_j|}\left(\partial N_{t_j}(P_i)\right) \times (0,t_{j-1}) \\ & = \left.\coprod_{\genfrac{}{}{0pt}{}{\sum \ell_i=n-k}{\ell_i \in \Z_{>0}}}\ \prod_{i=1}^k\ \coprod_{\genfrac{}{}{0pt}{}{\tau\in T(e)}{e\in E_{\ell_i}}}\left( \Ran^{|\tau_1|} (\partial N_{t_0}(P_i))\times \prod_{j=2}^{|\tau|} \Ran^{|\tau_j|}\left(\partial N_{t_j}(P_i)\right) \times (0,t_{j-1})\right) \times [0,\epsilon/2)\right/\sim \end{align*}$$
is an open cone based at $P$ sitting inside $\Ran^{\leqslant n}(M)$. Here $\sim$ is the equivalence relation of all elements with $t_0=0$, with $[0,\epsilon/2)\owns t_0$ representing the unit interval in the usual cone construction. Moreover, given the point-counting stratification $f:\Ran^{\leqslant n}(M)\to A$, there is a natural stratification $g:C_p\to A_{\geqslant f(P)}$, with $P\in C_P$ the only element mapping to $f(P)$ under $g$.

The next step is to show that $P$ has an open neighborhood in $\Ran^{\leqslant n}(M)$ that is the image of an open embedding $Z\times C_P$, for some topological space $Z$. The obvious choice $Z = \prod_{i=1}^k N_{\epsilon/2}(P_i)$ does not work, because we double count points in higher strata, so we do not have an embedding.

Exit paths, part 2

In this post we continue on a previous topic ("Exit paths, part 1," 2017-08-31) and try to define a constructible sheaf via universality. Let $X$ be an $A$-stratified space, that is, a topological space $X$ and a poset $(A,\leqslant)$ with a continuous map $f:X\to A$, where $A$ is given the upset topology relative to its ordering $\leqslant$. Recall the full subcategory $\Sing^A(X)\subseteq \Sing(X)$ of exit paths on an $A$-stratified space $X$.

Proposition: If $X\to A$ is conically stratified, $\Sing^A(X)$ is an $\infty$-category.

Briefly, a stratification $f:X\to A$ is conical if for every stratum there exists a particular embedding from a stratified cone into $X$ (see Lurie for "conical stratification" and Ayala, Francis, Tanaka for "conically smooth stratified space," which seem to be the same). We will leave confirming the described stratification as conical to a later post.

This proposition, given as part of Theorem A.6.4 in Lurie, has a very long proof, so is not repeated here. Lurie actually proves that the natural functor $\Sing^A(X)\to N(A)$ described below is a (inner) fibration, which implies the unique lifting property of $\Sing^A(X)$ via the unique lifting property of $N(A)$ (and we already know nerves are $\infty$-categories).

Example: The nerve of a poset is an $\infty$-category. Being a nerve, it is already immediate, but it is worthwhile to consider the actual construction. For example, if $A = \{a\leqslant b\leqslant c \leqslant d\}$ is the poset with the ordering $\leqslant$, then the pieces $N(A)_i$ are as below.

It is immediate that every 3-horn can only be filled in one unique way (as there is only one element of $N(A)_3$), as well as that every 2-horn can be filled in one unique way (as every sequence of two composable morphisms appears as a horn of exactly one element of $N(A)_2$).

In Appendix A.9 of Higher Algebra, Lurie says that there is an equivalence of categories $$(A\text{-constructible sheaves on }X)   \cong   \left[(A\text{-exit paths on }X),\mathcal S\right],$$ given that $X$ is conically stratified, and for $\mathcal S$ the $\infty$-category of spaces (equivalently $N(Kan)$, the nerve of all the simplicial sets that are Kan complexes). So, instead of trying to define  a particular constructible sheaf on $X = \Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$, (as in previous posts "Stratifying correctly," 2017-09-17 and "A constructible sheaf over the Ran space," 2017-06-24) we will try to make a functor that takes an exit path of $X$ and gives back a space.

Fix $n\in \Z_{>0}$ and set $X = \Ran^{\leqslant n}\times \R_{\geqslant 0}$. Let $SC$ be the category of simplicial complexes and simplicial maps, with $SC_n$ the full subcategory of simplicial complexes with at most $n$ vertices. There is a map
$$\begin{array}{r c l} g\ :\ X & \to & SC_n \\ (P,t) & \mapsto & VR(P,t), \end{array}$$
allowing us to say
$$X = \bigcup_{S\in SC_n}g^{-1}(S).$$
Here we consider that two elements $P_i,P_j\in P$ give an edge of $VR(P,t)$ whenever $t>d(P_i,P_j)$ (this is chosen instead of $t\geqslant d(P_i,P_j)$ so that the boundaries of the strata ``facing downward," with respect to the poset ordering, are open). Now we define a stratifying poset $A$ for $X$.

Definition: Let $A = \{a_S\ :\ S\in SC_n\}$ and define a relation $\leqslant$ on $A$ by
$$\left(a_S\leqslant a_T\right)\ \ \Longleftarrow\ \ \left( \begin{array}{c} \exists\ \sigma\in \Sing(X)_1\ \text{such that}\\ g(\sigma(0))=S,\ g(\sigma(t>0))=T. \end{array} \right)$$
Let $(A,\leqslant)$ be the poset generated by relations of the type given above.

We claim that $f:X\to A$ given by $f(P,t)=a_{g(P,t)}$ is a stratifying map, that is, continuous in the upset topology on $A$. To see this, take the open set $U_S = \{a_T\in A\ :\ a_S\leqslant a_T\}$ in the basis of the upset topology of $A$, for any $S\in SC_n$, and consider $x\in f^{-1}(U_S)$. If for all $\epsilon>0$ we have $B_X(x,\epsilon)\cap f^{-1}(U_S)^C\neq \emptyset$, then there exists $T_\epsilon\in SC_n$ with $B_X(x,\epsilon)\cap f^{-1}(a_{T_\epsilon})\neq\emptyset$, for $S\not\leqslant T_\epsilon$ (as $T_\epsilon\not\in U_S$). This means there exists $\sigma\in \Sing(X)_1$ with $\sigma(0)=x$ and $\sigma(t>0)\in f^{-1}(a_{T_\epsilon})$, which in turn implies $S\leqslant T_\epsilon$, a contradiction. Hence $f$ is continuous, so $f:X\to A$ is a stratification.

As all morphisms in $\Sing(X)$ are compsitions of the face maps $s_i$ and degenracy maps $d_i$, so are all morphisms in $\Sing^A(X)$. There is a natural functor $F:\Sing^A(X)\to N(A)$ defined in the following way:
$$\begin{array}{r r c l} %% %% L1 %% \text{objects} & \left( \begin{array}{c} \sigma:|\Delta^k|\to X \\ a_0\leqslant \cdots \leqslant a_k\subseteq A \\ f(\sigma(t_0,\dots,t_i\neq 0,0,\dots,0)) = a_i \end{array} \right) & \mapsto & \left( a_0\to\cdots\to a_k\in N(A)_k\right) \\[20pt] %% %% L2 %% \text{face maps} & \left( \begin{array}{c} \left( \begin{array}{c} \sigma:|\Delta^k|\to X \\ a_0\leqslant \cdots \leqslant a_k\subseteq A \end{array} \right)\\[10pt] \downarrow \\[10pt] \left( \begin{array}{c} \tau:|\Delta^{k+1}|\to X \\ a_0\leqslant \cdots \leqslant a_i\leqslant a_i\leqslant \cdots a_k\subseteq A \end{array} \right) \end{array} \right) & \mapsto & \left(\begin{array}{c} \left(a_0\to\cdots \to a_k\right)\\[10pt] \downarrow\\[10pt] \left(a_0\to\cdots \to a_i\xrightarrow{\text{id}}a_i\to\cdots \to a_k\right) \end{array}\right)\\[40pt] %% %% L3 %% \text{degeneracy maps} & \left( \begin{array}{c} \left( \begin{array}{c} \sigma:|\Delta^k|\to X \\ a_0\leqslant \cdots \leqslant a_k\subseteq A \end{array} \right)\\[10pt] \downarrow \\[10pt] \left( \begin{array}{c} \tau:|\Delta^{k-1}|\to X \\ a_0\leqslant \cdots \leqslant a_{i-1}\leqslant a_{i+1}\leqslant \cdots a_k\subseteq A \end{array} \right) \end{array} \right) & \mapsto & \left(\begin{array}{c} \left(a_0\to\cdots \to a_k\right)\\[10pt] \downarrow\\[10pt] \left(a_0\to\cdots \to a_{i-1}\xrightarrow{\circ}a_{i+1}\to\cdots \to a_k\right) \end{array}\right) \end{array}$$
As all maps in $\Sing^A(X)$ are generated by compositions of face and degeneracy maps, this completely defines $F$. Naturality of $F$ follows precisely because of this.

A poset (which can be viewed as a directed simple graph) may be naturally viewed as a 1-dimensional simplicial set, moreover an $\infty$-category (by virtue of being a \emph{simple} graph, with no multi-edges or loops). Hence there is a natural map, the inclusion, that takes $N(A)$ into $N(\mathcal Kan) = \mathcal S$.  Finally, Construction A.9.2 of Lurie describes a map that takes a functor from $A$-exit paths into spaces and gives back an $A$-constructible sheaf over $X$, which Theorem A.9.3 shows to be an equivalence, given the following conditions:

• $X$ is paracompact,
• $X$ is locally of singular shape,
• the $A$-stratification of $X$ is conical, and
• $A$ satisfies the ascending chain condition.

The first condition is satisfied as both $\Ran^{\leqslant n}(M)$ and $\R_{\geqslant 0}$ are locally compact and second countable. The last condition is satisfied because $A$ is a finite poset. We already mentioned that the conical property will be checked later, as will the singular shape property. Unfortunately, Lurie gives a definition of singular shape only for $\infty$-topoi, so some work must be done to translate this into our simpler setting. However, in the introduction to Appendix A, Lurie says that if $X$ is "sufficiently nice" and we assume some "mild assumptions" about $A$, then the described categorical equivalence follows, so it seems there is hope that everything will work out well in the end.

References: Stacks Project, Lurie (Higher algebra, Appendix A), Ayala, Francis and Tanaka (Local structures on stratified spaces, Sections 2 and 3)

Ordering simplicial complexes

In the context of trying to make a constructible sheaf over the Ran space, we have made several attempts to stratify $X=\Ran^{\leqslant n}(M)\times \R_{\geqslant0}$ correctly, the hope being for each stratum to have a unique simplicial complex (the Vietoris-Rips complex of the elements of $X$). In this post we make some observations and examine what it means to move around in $X$.

We use the convention that a Vietoris--Rips complex $VR(P,t)$ of an element $(P,t)\in X$ contains an edge $(P_i,P_j)$ iff $d(P_i,P_j)>t$ (as opposed to $d(P_i,P_j)\geqslant t$).

Observation 1: The VR complex $VR(P,t)$ is completely described by its 1-skeleton $sk_1(VR(P,t))$, as having a complete subgraph $K_\ell\subseteq sk_1(VR(P,t))$ is equivalent to $VR(P,t)$ having an $(\ell-1)$-cell spanning that subgraph. The 1-skeleton is a simple graph $G=(V,E)$ on $k$ vertices, so if we can order simple graphs with $\leqslant n$ vertices, we can order VR complexes of $\leqslant n$ vertices.

Let $\Gamma_k$ be the collection of simple gaphs on $k$ vertices. From now on we talk about an element $(P=\{P_1,\dots,P_k\},t)\in X$, a $k$-vertex VR complex $S=VR(P,t)$, and its 1-skeleton $G=sk_1(VR(P,t))\in \Gamma_k$ interchangeably. Consider the following informal defintion of how the stratification of $X$ should work.

Definition: A VR complex $S$ is ordered lower than another VR complex $T$ if there is a path from the stratum of type $S$ to the stratum of type $T$ that does not pass through strata of type $R$ with $|V(R)|<|V(S)|$ or $|E(R)|<|E(S)|$. If $S$ is ordered lower than $T$ and we can move from the stratum of type $S$ to the stratum of type $T$ without passing through another stratum, then we say that $S$ is directly below $T$.

To gain intuition of what this ordering means, consider the ordering on the posets $B_k'$, as defined in a previous post ("Stratifying correctly," 2017-09-17) and the 1-skeleta of the VR-complexes mapped to their elements. A complete description for $k=1,2,3,4$ and partially for $k=5$ is given below, with arrows $S\to T$ indicating the minimal number of directly below relationships. That is, if $S\to R$ but also $S\to T$ and $T\to R$, then $S\to R$ is not drawn.

The orderings on each $B_k'$ are clear and can be found in an algorithmic manner. However, it is more difficult to see which $S$ at level $k$ are directly below which $T$ at level $k+1$. The green arrows follow no clear pattern.

Observation 2: If $G\in \Gamma_k$ has an isolated vertex and $t>0$, then it can be directly below $H\in \Gamma_{k+1}$ only if $|E(H)|=|E(G)|+1$. In general, if the smallest degree of a vertex of $G\in \Gamma_k$ is $d$ and $t>0$, then $G$ can be directly below $H\in \Gamma_{k+1}$ only if $|E(H)|=|E(G)|+d+1$.

Recall the posets $B_k'$ are made by quotienting the nodes of the hypercube $B_k=\{0,1\}^{k(k-1)/2}$ by the action of $S_k$, where an element of $B_k$ is viewed as a graph $G\in \Gamma_k$ having an edge $(i,j)$ if the coordinate corresponding to the edge $(i,j)$ is 1 (there are $k(k-1)/2$ pairs $(i,j)$ of a $k$-element set).

Observation 3: It is not clear that $G$ not being ordered lower than $H$ in the hypercube context (order increases when increasing in any coordinate) implies that the VR complex of $G$ is not ordered lower than the VR complex of $H$ in $X$. No counterexample exists in the example given above, but this does not seem to exclude the possibility.

If any conclusion can be made from this, it is that this may not be the best approach to take when stratifying $X$.

Stratifying correctly

In a previous blog post ("A constructible sheaf over the Ran space," 2017-06-24) it was claimed that there was a particular constructible sheaf over $\Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$. However, the proof actually uses finite ordered subsets of $M$ to make the stratification, rather than finite unordered subsets. This means that the sheaf is actually over $M^{\times n}\times \R_{\geqslant 0}$, and in this post we try to fix that problem.

Let $\Delta_n$ be the "fat diagonal" of $M^{\times n}$, that is, the collection of $P\in M^{\times n}$ for which at least two coordinates are the same. For every $k>0$, there is an $S_k$ action on $M^{\times k}\setminus \Delta_k$, quotienting by which we get a map
$$M^{\times k}\setminus \Delta_k \xrightarrow{\ q_k\ }\Ran^k(M)$$
to the Ran space of degree $k$. The stratification of $M^{\times k}\times \R_{\geqslant 0}$ given in the previous post will be pushed forward to a stratification of $\Ran^k(M)\times \R_{\geqslant 0}$, for all $0<k\leqslant n$. A large part of the work already has been done, it remains to put everything in the right order and check openness. The process is given as follows:

1. Stratify $\Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$ into $n$ pieces, each being $\Ran^k(M)\times \R_{\geqslant 0}$.
2. Stratify $(M^{\times k}\setminus \Delta_k)\times \R_{\geqslant 0}$ as in the previous post.
3. Quotient by $S_k$-action to get stratification of $\Ran^k(M)\times \R_{\geqslant 0}$.

Step 1

As stated in the proof of the Theorem, $\Ran^{\geqslant k}(M)\times \R_{\geqslant 0}$ is open inside $\Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$, allowing us to make a stratification $f:\Ran^{\leqslant n}(M)\times \R_{\geqslant 0}\to A$, where $A$ is the poset

 

where the tail of an arrow is ordered lower than the head. The map $f$ sends $\Ran^k(M)\times \R_{\geqslant 0}$ to $a_k$, which is a continuous map in the upset topology on $A$.

Step 2

As stated in Definition 5, we have a stratification $g_k:(M^{\times k}\setminus \Delta_k) \times \R_{\geqslant 0}\to B_k$, where $B_k$ may be viewed as a directed graph $B_k=(V_k,E_k)$. The vertex set is $V_k = \{0,1\}^{k(k+1)/2}$, whose elements are strings of 1 and 0, and the edge set $E_k$ contains $v\to v'$ iff $d_H(v,v')=1$ and $d_H(v,0)<d_H(v',0)$, for $d_H$ the Hamming distance. Let $U_v\subset B_k$ denote the upset based at $v$, that is, all elements $v'\in B_k$ with $v\leqslant v'$.

Order all distinct pairs $(i,j)\in \{1,\dots,k\}^2$, of which there are $k(k+1)/2$. Under the stratifying map $g_k$, each upset $U_v$ based at the vertex $v\in\{0,1\}^{k(k+1)/2}$ receives elements $(P,t)\in (M^{\times k}\setminus \Delta_k)\times \R_{\geqslant 0}$ satisfying $t>d(P_i,P_j)$ whenever the position representing $(i,j)$ in $v$ is 1. For example, when $k=3$,

To check that $g_k$ is continuous in the upset topology, we restate Lemma 2 in a clearer way.

Lemma 1: Let $U\subset X$ be open and $\varphi:X\to A\subset \R_{\geqslant 0}$ continuous, with $|A|<\infty$. Then
$$\bigcup_{x\in U}\{x\}\times (\varphi(x),\infty)\ \subseteq\ X\times (z',\infty)$$
is open, for any $z'\leqslant z:= \min_{x\in U}\{\varphi(x)\}$.

Proof: Consider the function
$$\begin{array}{r c l} \psi\ :\ X\times (z',\infty) & \to & X\times (-\infty,z), \\ (x,t) & \mapsto & (x,\varphi(x)-t). \end{array}$$
Since $\varphi$ is continuous and subtraction is continuous, $\psi$ is continuous (in the product topology). Since $U\times (-\infty,0)$ is open in $X\times (-\infty,z)$, the set $\psi^{-1}(U\times (-\infty,0))$ is open in $X\times (z',\infty)$. For any $x\in U$ and $t=\varphi(x)$, we have $\varphi(x)-t =0$. For any $x\in U$ and $t\to \infty$, we have $\varphi(x)-t\to -\infty$. It is immediate that all other $t\in (\varphi(x),\infty)$ give $\varphi(x)-t\in (-\infty,0)$. Hence $\psi^{-1}(U\times (-\infty,0))$ is the collection of points $(x,t)$ with $t\in (\varphi(x),\infty)$, which is then open in $X\times [0,z')$. $\square$

Applying Lemma 1 to $U=X=M^{\times k}\setminus \Delta_k$ and $\varphi(P) = \max_{i\neq j}\{d(P_i,P_j)\}$, which is continuous, gives that $g_k^{-1}(U_{11\cdots1})\subseteq M^{\times k}\setminus \Delta_k$ is open. This also works to show that $g_k^{-1}(U_v)\subseteq g_k^{-1}(U_{v'})$ is open, for any $v'\leqslant v$, by limiting the pairs of indices iterated over by the function $\varphi$. Hence $g_k$ is continuous.

Step 3

The symmetric group $S_k$ acts on $(M^{\times k}\setminus \Delta_k)\times \R_{\geqslant 0}$ by permuting the order of elements in the first factor. That is, for $\sigma\in S_k$, we have
$$\sigma (P=\{P_1,\dots,P_k\},t) = (\{P_{\sigma(1)},\dots,P_{\sigma(k)}\},t).$$
Note that $((M^{\times k}\setminus \Delta_k)\times \R_{\geqslant 0})/S_k = \Ran^k(M)\times \R_{\geqslant 0}$.

Remark: Graph isomorphism for two graphs with $k$ vertices may also be viewed as the equivalence relation induced by $S_k$ acting on $\Gamma_k = \{$simple vertex-labeled graphs with $k$ vertices$\}$. First, let $G_v$ be the (unique) graph first introduced at element $v\in B_k$ by $g_k$. That is, we have $G_v =VR(P,t)_1$ (the ordered 1-skeleton of the Vietoris--Rips complex on the set $P$ with radius $t$) whenever $g_k((P,t))\in U_v$ and $g_k((P,t))\not\in U_{v'}$ for any $v'\leqslant v$, $v'\neq v$. Then the elements of $B_k$ are in bijection with the elements of $\Gamma_k$ (given by $v\leftrightarrow G_v$), so we have $B_k/S_k = B_k'$. Recall that $v\leqslant v'$ in $B_k$ iff adding an edge to $G_v$ gives $G_{v'}$. In $B_{k'}$, this becomes a partial order on equivalence classes $[w] = \{v\in B_k\ :\ \sigma G_v=G_w\ $for some $\sigma\in S_k\}$. We write $[w]\leqslant [w']$ iff there is a collection of pairs $\{(v_1,v_1'),\dots,(v_\ell,v_\ell')\}$ such that $v_i\leqslant v_i'$ for all $i$, and $\{v_1,\dots,v_\ell\} = [w]$ and $\{v_1',\dots,v_\ell'\} = [w']$ (there may be repetition among the $v_i$ or $v_i'$).

By the universal property of the quotient, there is a unique map $h_k:\Ran^k(M)\times \R_{\geqslant 0}\to B_k'$ that makes the following diagram commute.

This will be our stratifying map. To check that $h_k$ is continuous take $U\subseteq B_k'$ open. As $\pi$ is the projection under a group action, it is an open map, so $\pi^{-1}(U)\subseteq B_k$ is open. Since $g_k$ is continuous in the upset topology, $g_k^{-1}(\pi^{-1}(U))$ is open. Again, $S_k\curvearrowright$ is the projection under a group action, so $(S_k\curvearrowright)(g_k^{-1}(\pi^{-1}(U)))$ is open, giving continuity of $h_k$.

Exit paths, part 1

This post is meant to set up all the necessary ideas to define the category of exit paths.

Preliminaries

 Let $X$ be a topological space and $C$ a category. Recall the following terms:

• $\Delta$: The category whose objects are finite ordered sets $[n]=(1,\dots,n)$ and whose morphisms are non-decreasing maps. It has several full subcategories, including
  • $\Delta_s$, comprising the same objects of $\Delta$ and only injective morphisms, and
  • $\Delta_{\leqslant n}$, comprising only the objects $[0],\dots,[n]$ with the same morphisms.
• equalizer: An object $E$ and a universal map $e:E\to X$, with respect to two maps $f,g:X\to Y$. It is universal in the sense that all maps into $X$ whose compositions with $f,g$ are equal factor through $e$. Equalizers and coequalizers are described by the diagram below, with universality given by existence of the dotted maps.

• fibered product or pullback: The universal object $X\times_Z Y$ with maps to $X$ and $Y$, with respect to maps $X\to Z$ and $Y\to Z$.
• fully faithful: A functor $F$ whose morphism restriction $\Hom(X,Y)\to \Hom(F(X),F(Y))$ is surjective (full) and injective (faithful).
• locally constant sheaf: A sheaf $\mathcal F$ over $X$ for which every $x\in X$ has a neighborhood $U$ such that $\mathcal F|_U$ is a constant sheaf. For example, constructible sheaves are locally constant on every stratum. 
• simplicial object: A contravariant functor from $\Delta$ to any other category. When the target category is $\text{Set}$, it is called a simplicial set. They may also be viewed as a collection $S = \{S_n\}_{\geqslant 0}$ for $S_n=S([n])$ the value of the functor on each $[n]$. Simplicial sets come with two natural maps:
  • face maps $d_i:S_n\to S_{n-1}$ induced by the map $[n-1]\to [n]$ which skips the $i$th piece, and
  • degeneracy maps $s_i:S_n\to S_{n+1}$ induced by the map $[n+1]\to[n]$ which repeats the $i$th piece.
• stratification: A property of a cover $\{U_i\}$ of $X$ for which consecutive differences $U_{i+1}\setminus U_i$ have ``nicer" properties than all of $X$. For example, $E_i\to U_{i+1}\setminus U_i$ is a rank $i$ vector bundle, but there is no vector bundle $E\to X$ that restricts to every $E_i$.

Now we get into new territory.

Definition: The nerve of a category $C$ is the collection $N(C) = \{N(C)_n = Fun([n],C)\}_{n\geqslant 0}$, where $[n]$ is considered as a category with objects $0,\dots,n$ and a single morphism in $\Hom_{[n]}(s,t)$ iff $s\leqslant t$.

Note that the nerve of $C$ is a simplicial set, as it is a functor from $\Delta^{op}\to Fun(\Delta,C)$. Moreover, the pieces $N(C)_0$ are the objects of $C$ and $N(C)_1$ are the morphisms of $C$, so all the information about $C$ is contained in its nerve. There is more in the higher pieces $N(C)_n$, so the nerve (and simplicial sets in general) may be viewed as a generalization of a category.

Kan structures

Let $\text{sSet}$ be the category of simplicial sets. We may consider $\Delta^n = \Hom_\Delta(-,[n])$ as a contravariant functor $\Delta\to \text{Set}$, so it is an object of $\text{sSet}$.

Definition: Fix $n\geqslant 0$ and choose $0\leqslant i\leqslant n$. Then the $i$th $n$-horn of a simplicial set is the functor $\Lambda^n_i\subset \Delta^n$ generated by all the faces $\Delta^n(d_j)$, for $j\neq i$.

We purposefully do not describe what "$\subset$" or "generated by" mean for functors, hoping that intuition fills in the gaps. In some sense the horn feels like a partially defined functor (though it is a true simplicial set), well described by diagrams, for instance with $n=2$ and $i=1$ we have

Definition: A simplicial set $S$ is a Kan complex whenever every map $f:\Lambda^n_i\to S$ factors through $\Delta^n$. That is, when there exists a

The map $\iota$ is the inclusion. Moreover, $S$ is an $\infty$-category, or quasi-category, if the extending map $f'$ is unique.

Example: Some basic examples of $\infty$-categories, for $X$ a topological space, are

• $Sing(X)$, made up of pieces $Sing(X)_n = \Hom(\Delta^n,X)$, and
• $LCS(X)$, the category of locally constant sheaves over $X$. Here $LCS(X)_n$ over an object $A$, whose objects are $B\to A$ and morphisms are the appropriate commutative diagrams

Definition: A morphism $p\in \Hom_{\text{sSet}}(S,T)$ is a Kan fibration if for every commutative diagram (of solid arrows)

the dotted arrow exists, making the new diagram commute.

Definition: Let $C,D,A$ be categories with functors $F:C\to D$ and $G:C\to A$.

• The left Kan extension of $F$ along $G$ is a functor $A\xrightarrow L D$ and a universal natural transformation $F\stackrel \lambda \rightsquigarrow L\circ G$.
• The right Kan extension of $F$ along $G$ is a functor $A\xrightarrow R D$ and a universal natural transformation $R\circ G \stackrel \rho\rightsquigarrow F$.

Exit paths

The setting for this section is constructible sheaves over a topological space $X$. We begin with a slightly more technical definition of a stratification.

Definition: Let $(A,\leqslant)$ be a partially ordered set with the upset topology. That is, if $x\in U$ is open and $x\leqslant y$, then $y\in A$. An $A$-stratification of $X$ is a continuous function $f:X\to A$.

We now begin with a Treumann's definition of an exit path, combined with Lurie's stratified setting.

Definition: An exit path in an $A$-stratified space $X$ is a continuous map $\gamma:[0,1]\to X$ for which there exists a pair of chains $a_1\leqslant \cdots \leqslant a_n$ in $A$ and $0=t_0\leqslant \cdots \leqslant t_n=1$ in $[0,1]$ such that $f(\gamma(t))=a_i$ whenever $t\in (t_{i-1},t_i]$.

This really is a path, and so gives good intuition for what is happening. Recall that the geometric realization of the functor $\Delta^n$ is $|\Delta^n| = \{(t_0,\dots,t_n)\in \R^{n+1}\ :\ t_0+\cdots+t_n=1\}$. Oserving that $[0,1]\cong|\Delta^1|$, Lurie's definition of an exit path is more general by instead considering maps from $|\Delta^n|$.

Definition: The category of exit paths in an $A$-stratified space $X$ is the simplicial subset $Sing^A(X)\subset Sing(X)$ consisting of those simplices $\gamma:|\Delta^n|\to X$ for which there exists a chain $a_0\leqslant \cdots \leqslant a_n$ in $A$ such that $f(\gamma(t_0,\dots,t_i,0,\dots,0))=a_i$ for $t_i\neq 0$.

Example: As with all new ideas, it is useful to have an example. Consider the space $X=\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$ of a closed manifold $M$ (see post "A constructible sheaf over the Ran space" 2017-06-24 for more). With the poset $(A,\leqslant)$ being $(a\leqslant b\leqslant c)$ and stratifying map
$$\begin{array}{r c l} f\ :\ X & \to & A, \\ (P,t) & \mapsto & \begin{cases} a & \text{ if } P\in \Ran^1(M), \\ b & \text{ if } P\in \Ran^2(M), t\leqslant d(P_1,P_2), \\ c & \text{ else,} \end{cases} \end{array}$$
we can make a continuous map $\gamma:\Delta^3\to X$ by
$$\begin{array}{r c l} (1,0,0) & \mapsto & (P\in \Ran^1(M),0), \\ (t_0,t_1\neq 0,0) & \mapsto & (P\in \Ran^2(M), d(P_1,P_2)), \\ (t_0,t_1,t_2\neq 0) & \mapsto & (P\in \Ran^2(M), t>d(P_1,P_2)). \end{array}$$
Then $f(\gamma(t_0\neq 0,0,0))=a$, and $f(\gamma(t_0,t_1\neq 0,0))=b$, and $f(\gamma(t_0,t_1,t_2\neq 0))=c$, as desired. The embedding of such a simplex $\gamma$ is described by the diagram below.

Both the image of $(1,0,0)$ and the 1-simplex from $(1,0,0)$ to $(0,1,0)$ lie in the singularity set of $\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$, which is pairs $(P,t)$ where $t=d(P_i,P_j)$ for some $i,j$. The idea that the simplex "exits" a stratum is hopefully made clear by this image.

References: Lurie (Higher algebra, Appendix A), Lurie (What is... an $\infty$-category?), Groth (A short course on $\infty$-categories, Section 1), Joyal (Quasi-categories and Kan complexes), Goerss and Jardine (Simplicial homotopy theory, Chapter 1), Treumann (Exit paths and constructible stacks)

The Ran space and singularity sets

Fix a manifold $M$ along with an embedding of $M$ into $\R^N$ and set $X=\Ran(M)\times \R_{\geqslant 0}$. The goal of this post is to show that every $(P,t)\in X$ has an open neighborhood that contains no points of the type $(Q,d(Q_i,Q_j))$, for some $i\neq j$. The collection of all such elements of $X$ is called the singularity set of $X$, as the Vietoris-Rips complex at $Q$ with such a radius changes at such elements.

Following Lurie, given a collection of open sets $\{U_i\}_{i=1}^k$ in $M$, set
$$\Ran(\{U_i\}_{i=1}^k) = \left\{P\in \Ran(M)\ :\ P\subset \bigcup_{i=1}^k U_i,\ P\cap U_i\neq \emptyset\ \forall\ i\right\}.$$
The topology on $\Ran(M)$ is the smallest topology for which every $\Ran(\{U_i\}_{i=1}^k)$ is open, for any $\{U_i\}_{i=1}^k$, for any $k$. The topology on the product $X$ is the product topology.

Remark: Note that the Ran space $\Ran(M)$ by itself can be split up into the pieces $\Ran^k(M)$, with "singularities" viewed as when a point splits into two (or more) points, or two (or more) combine into one. Then every element of $\Ran(M)$ is on the edge of the singularity set, as any neighborhood of a single point on the manifold contains two points on the manifold.

Fix $(P,t)\in X$ not in the singularity set of $X$, with $P=(P_1,\dots,P_k)$, for $1\leqslant k\leqslant n$. Set
$$\mu = \min\left\{t,\min_{1\leqslant i<j\leqslant k}\left\{|t-d(P_i,P_j)|\right\}\right\},$$
with distance $d$ being Euclidean distance in $\R^N$. The quantity $\mu$ should be thought of as the upper bound on how "far" we may move from $(P,t)$ without hitting the singularity set.

Proposition: Let $(P,t)$ be as above and $t,\alpha,\beta>0$ such that $\alpha+\beta=\mu$. Then
$$U=\Ran\left(\{B(P_i,\alpha/2)\}_{i=1}^k\right) \times \left(t-\beta,t+\beta\right)$$
is an open neighborhood of $(P,t)$ in $X$ and does not contain any points of the singularity set of $X$.

If $t=0$, then having $[0,\beta)$ as the second component of $U$, with $\alpha+\beta=\min_{i,j}d(P_i,P_j)$ works as the open neighborhood of $(P,t)$. The balls $B(x,r)$ are $N$-dimensional in $\R^N$. The proof is mostly applications of the triangle inequality.

Proof: By construction we have that $U$ is open in $X$ and that it contains $(P,t)$. For $(Q,s)\in U$ any other element, we have three cases. We will show that the distance between any two $Q_a,Q_b\in Q$ is never $s$. Fix distinct indices $\ell,m\in \{1,\dots,k\}$.

1.  Case 1: $Q_a,Q_b\in B(P_\ell,\alpha/2)$. The situation looks as in the diagram below.
   
   Observe that $d(Q_a,Q_b)\leqslant d((Q_a,P_\ell)+d(Q_b,P_\ell) <\alpha = \mu-\beta \leqslant t-\beta$. Hence $d(Q_a,Q_b)<s$.
2. Case 2: $Q_a\in B(P_\ell,\alpha/2), Q_b\in B(P_m,\alpha/2), d(P_\ell,P_m)>t$. The situation looks as in the diagram below.
   
   Observe that $d(P_\ell,P_m)\leqslant d(P_\ell,Q_b)+d(P_m,Q_b)\leqslant d(P_\ell,Q_a)+d(Q_a,Q_b)+d(P_m,Q_b) < \alpha+d(Q_a,Q_b)$. Since $d(P_\ell,P_m)>t$, the definition of $\mu$ gives us that $\mu \leqslant d(P_\ell,P_m)-t$, so combining this with the previous inequality, we get $d(Q_a,Q_b) > d(P_\ell,P_m)-\alpha\geqslant \mu+t-(\mu-\beta)=t+\beta$. Hence $d(Q_a,Q_b)>s$.
3. Case 3: $Q_a\in B(P_\ell,\alpha/2), Q_b\in B(P_m,\alpha/2), d(P_\ell,P_m)<t$. The situation looks as in the diagram below.
   
   Observe that $d(Q_a,Q_b)\leqslant d(P_m,Q_b) + d(P_m,Q_a) \leqslant d(P_\ell,Q_a)+d(P_\ell,P_m)+d(P_m,Q_a)<\alpha+d(P_\ell,P_m)$. Since $d(P_\ell,P_m)<t$, the definition of $\mu$ gives us that $\mu\leqslant t-d(P_\ell,P_m)$, so combining this with the previous inequality, we get $d(Q_a,Q_b)<\mu-\beta+t-\mu = t-\beta$. Hence $d(Q_a,Q_b)<s$. $\square$

As an extension, it would be nice to show that the Vietoris--Rips complex of every element in $U$ is homotopy equivalent. This seems to be intuitively true, but a similar case analysis as above seems daunting.

References: Lurie (Higher Algebra, Section 5.5.1)