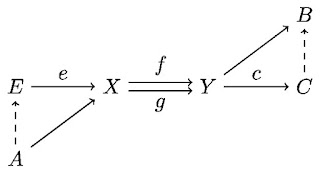Exit paths and entry paths through $\infty$-categories

Let $X$ be a topological space, $(A,\leqslant)$ a poset, and $f: X\to (A,\leqslant)$ a continuous map.

Definition: An exit path in an $A$-stratified space $X$ is a continuous map $\sigma: |\Delta^n|\to X$ for which there exists a chain $a_0\leqslant \cdots \leqslant a_n$ in $A$ such that $f(\sigma(t_0,\dots,t_i,0,\dots,0))=a_i$ for $t_i\neq 0$. An entry path is a continuous map $\tau: |\Delta^n|\to X$ for which there exists a chain $b_0\leqslant \cdots \leqslant b_n$ in $A$ such that $f(\tau(0,\dots,0,t_i,\dots,t_n))=b_i$ for $t_i\neq 0$.

Up to reordering of vertices of $\Delta^n$ and induced reordering of the realization $|\Delta^n|$, an exit path is the same as an entry path. The next example describes this equivalence.

Example: The standard 2-simplex $|\Delta^2|$ is uniquely an exit path and an entry path with a chain of 3 distinct elements, stratfied in the ways described below.

Recall the following algebraic constructions, through Joyal's quasi-category model:

• A simplicial set is a functor $\Delta^{op}\to \Set$.
• A Kan complex is a simplicial set satisfying the inner horn condition for all $0\leqslant k\leqslant n$. That is, the $k$th $n$-horn lifts (can be filled in) to a map on $\Delta^n$.
• An $\infty$-category is a simplicial set satisfying the inner horn condition for all $0<k<n$.

Moreover, if the lift is unique, then the Kan complex is the nerve of some category. Recall also the category $\Sing(X) = \{$continuous $\sigma: |\Delta^n|\to X\}$, which can be combined with the stratification $f: X\to A$ of $X$

Remark: The subcategory $\Sing^A(X)$ of exit paths and the subcategory $\Sing_A(X)$ of entry paths are full subcategories of $\Sing(X)$, with $(\Sing^A(X))^{op} = \Sing_A(X)$. If the stratification is conical, then these two categories are $\infty$-categories.

Recall the nerve construction of a category. Here we are interested in the nerve of the category $SC$ of simplicial complexes, so $N(SC)_n = \{$sequences of $n$ composable simplicial maps$\}$. Recall the $k$th $n$-horns, which are compatible diagrams of elements of $N(SC)_n$. In general, they are colimits of a diagram in the category $\Delta$. That is, \[ \Lambda^n_k := \colim \left(\bigsqcup_{0\leqslant i<j\leqslant n} \Delta^{n-2} \rightrightarrows \bigsqcup_{0\leqslant i\leqslant n \atop i\neq k} \Delta^{n-1}\right). \] Example: The images of the 3 different types of 2-horns and 4 different types of 3-horns in $SC$ are given below. Note that they are not unique, and depend on the choice of simplices $S_i$ (equivalently, on the choice of functor $\Delta^{op}\to SC$).

For example, the 0th 2-horn $\Lambda^2_0$ can be filled in if there exists a simplicial map $h: S_1\to S_2$ in $SC$ (that is, an element of $N(SC)_1$) such that $h\circ f = g$. Similarly, the 1st 3-horn $\Lambda^3_1$ can be filled in if there exists a functor $F: [0<1<2]\to SC$ for which $F(0<1)=f_{02}$, $F(0<2)=f_{03}$, and $F(1<2)=f_{23}$ (equivalently, a compatible collection of elements of $N(SC)_2$).

Definition: Let $A,B$ be $\infty$-categories. A functor $F: A\to B$ is a morphism of the simplicial sets $A,B$. That is, $F:A\to B$ is a natural transformation for $A,B\in \text{Fun}(\Delta^{op},\Set)$.

A functor of simplicial sets of a particular type can be identified with a functor of 1-categories. Recall the nerve of a 1-category, which turns it into an $\infty$-category. This construction has a left adjoint.

Definition: Let $\mathcal C$ be an $\infty$-category. The homotopy category $h\mathcal C$ of $\mathcal C$ has objects $\mathcal C_0$ and morphisms $\Hom_{h\mathcal C}(X,Y) = \pi_0(\text{Map}_{\mathcal C}(X,Y))$.

By Lurie, $h$ is left-adjoint to $N$. That is, $h : \sSet \rightleftarrows \text{Cat} : N$, or $\text{Map}_{\sSet}(\mathcal C,N(\mathcal D)) \cong \text{Map}_{\text{Cat}}(h\mathcal C, \mathcal D)$, for any $\infty$-category $\mathcal C$ and any 1-category $\mathcal D$. Our next goal is to describe a functor $\Sing_A(X)\to N(SC)$, maybe through this adjunction, where $SC$ is the 1-category of simplicial complexes and simplicial maps.

References: Lurie (Higher topos theory, Sections 1.1.3 and 1.2.3), Lurie (Higher algebra, Appendix A.6), Goerss and Jardine (Simplicial homotopy theory, Section I.3), Joyal (Quasi-categories and Kan complexes)

Exit paths, part 2

In this post we continue on a previous topic ("Exit paths, part 1," 2017-08-31) and try to define a constructible sheaf via universality. Let $X$ be an $A$-stratified space, that is, a topological space $X$ and a poset $(A,\leqslant)$ with a continuous map $f:X\to A$, where $A$ is given the upset topology relative to its ordering $\leqslant$. Recall the full subcategory $\Sing^A(X)\subseteq \Sing(X)$ of exit paths on an $A$-stratified space $X$.

Proposition: If $X\to A$ is conically stratified, $\Sing^A(X)$ is an $\infty$-category.

Briefly, a stratification $f:X\to A$ is conical if for every stratum there exists a particular embedding from a stratified cone into $X$ (see Lurie for "conical stratification" and Ayala, Francis, Tanaka for "conically smooth stratified space," which seem to be the same). We will leave confirming the described stratification as conical to a later post.

This proposition, given as part of Theorem A.6.4 in Lurie, has a very long proof, so is not repeated here. Lurie actually proves that the natural functor $\Sing^A(X)\to N(A)$ described below is a (inner) fibration, which implies the unique lifting property of $\Sing^A(X)$ via the unique lifting property of $N(A)$ (and we already know nerves are $\infty$-categories).

Example: The nerve of a poset is an $\infty$-category. Being a nerve, it is already immediate, but it is worthwhile to consider the actual construction. For example, if $A = \{a\leqslant b\leqslant c \leqslant d\}$ is the poset with the ordering $\leqslant$, then the pieces $N(A)_i$ are as below.

It is immediate that every 3-horn can only be filled in one unique way (as there is only one element of $N(A)_3$), as well as that every 2-horn can be filled in one unique way (as every sequence of two composable morphisms appears as a horn of exactly one element of $N(A)_2$).

In Appendix A.9 of Higher Algebra, Lurie says that there is an equivalence of categories \[(A\text{-constructible sheaves on }X)   \cong   \left[(A\text{-exit paths on }X),\mathcal S\right],\] given that $X$ is conically stratified, and for $\mathcal S$ the $\infty$-category of spaces (equivalently $N(Kan)$, the nerve of all the simplicial sets that are Kan complexes). So, instead of trying to define  a particular constructible sheaf on $X = \Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$, (as in previous posts "Stratifying correctly," 2017-09-17 and "A constructible sheaf over the Ran space," 2017-06-24) we will try to make a functor that takes an exit path of $X$ and gives back a space.

Fix $n\in \Z_{>0}$ and set $X = \Ran^{\leqslant n}\times \R_{\geqslant 0}$. Let $SC$ be the category of simplicial complexes and simplicial maps, with $SC_n$ the full subcategory of simplicial complexes with at most $n$ vertices. There is a map
\[\begin{array}{r c l}
g\ :\ X & \to & SC_n \\
(P,t) & \mapsto & VR(P,t),
\end{array}\]
allowing us to say
\[X = \bigcup_{S\in SC_n}g^{-1}(S).\]
Here we consider that two elements $P_i,P_j\in P$ give an edge of $VR(P,t)$ whenever $t>d(P_i,P_j)$ (this is chosen instead of $t\geqslant d(P_i,P_j)$ so that the boundaries of the strata ``facing downward," with respect to the poset ordering, are open). Now we define a stratifying poset $A$ for $X$.

Definition: Let $A = \{a_S\ :\ S\in SC_n\}$ and define a relation $\leqslant$ on $A$ by
\[ \left(a_S\leqslant a_T\right)\ \ \Longleftarrow\ \ \left(
\begin{array}{c}
\exists\ \sigma\in \Sing(X)_1\ \text{such that}\\
g(\sigma(0))=S,\ g(\sigma(t>0))=T.
\end{array}
\right)\]
Let $(A,\leqslant)$ be the poset generated by relations of the type given above.

We claim that $f:X\to A$ given by $f(P,t)=a_{g(P,t)}$ is a stratifying map, that is, continuous in the upset topology on $A$. To see this, take the open set $U_S = \{a_T\in A\ :\ a_S\leqslant a_T\}$ in the basis of the upset topology of $A$, for any $S\in SC_n$, and consider $x\in f^{-1}(U_S)$. If for all $\epsilon>0$ we have $B_X(x,\epsilon)\cap f^{-1}(U_S)^C\neq \emptyset$, then there exists $T_\epsilon\in SC_n$ with $B_X(x,\epsilon)\cap f^{-1}(a_{T_\epsilon})\neq\emptyset$, for $S\not\leqslant T_\epsilon$ (as $T_\epsilon\not\in U_S$). This means there exists $\sigma\in \Sing(X)_1$ with $\sigma(0)=x$ and $\sigma(t>0)\in f^{-1}(a_{T_\epsilon})$, which in turn implies $S\leqslant T_\epsilon$, a contradiction. Hence $f$ is continuous, so $f:X\to A$ is a stratification.

As all morphisms in $\Sing(X)$ are compsitions of the face maps $s_i$ and degenracy maps $d_i$, so are all morphisms in $\Sing^A(X)$. There is a natural functor $F:\Sing^A(X)\to N(A)$ defined in the following way:
\[\begin{array}{r r c l}
%%
%% L1
%%
\text{objects} & \left(
\begin{array}{c}
\sigma:|\Delta^k|\to X \\
a_0\leqslant \cdots \leqslant a_k\subseteq A \\
f(\sigma(t_0,\dots,t_i\neq 0,0,\dots,0)) = a_i
\end{array}
\right) & \mapsto & \left( a_0\to\cdots\to a_k\in N(A)_k\right) \\[20pt]
%%
%% L2
%%
\text{face maps} & \left(
\begin{array}{c}
\left(
\begin{array}{c}
\sigma:|\Delta^k|\to X \\ a_0\leqslant \cdots \leqslant a_k\subseteq A
\end{array}
\right)\\[10pt]
\downarrow \\[10pt]
\left(
\begin{array}{c}
\tau:|\Delta^{k+1}|\to X \\ a_0\leqslant \cdots \leqslant a_i\leqslant a_i\leqslant \cdots a_k\subseteq A
\end{array}
\right)
\end{array}
\right) & \mapsto &
\left(\begin{array}{c}
\left(a_0\to\cdots \to a_k\right)\\[10pt]
\downarrow\\[10pt]
\left(a_0\to\cdots \to a_i\xrightarrow{\text{id}}a_i\to\cdots \to a_k\right)
\end{array}\right)\\[40pt]
%%
%% L3
%%
\text{degeneracy maps} & \left(
\begin{array}{c}
\left(
\begin{array}{c}
\sigma:|\Delta^k|\to X \\ a_0\leqslant \cdots \leqslant a_k\subseteq A
\end{array}
\right)\\[10pt]
\downarrow \\[10pt]
\left(
\begin{array}{c}
\tau:|\Delta^{k-1}|\to X \\ a_0\leqslant \cdots \leqslant a_{i-1}\leqslant a_{i+1}\leqslant \cdots a_k\subseteq A
\end{array}
\right)
\end{array}
\right) & \mapsto &
\left(\begin{array}{c}
\left(a_0\to\cdots \to a_k\right)\\[10pt]
\downarrow\\[10pt]
\left(a_0\to\cdots \to a_{i-1}\xrightarrow{\circ}a_{i+1}\to\cdots \to a_k\right)
\end{array}\right)
\end{array}\]
As all maps in $\Sing^A(X)$ are generated by compositions of face and degeneracy maps, this completely defines $F$. Naturality of $F$ follows precisely because of this.

A poset (which can be viewed as a directed simple graph) may be naturally viewed as a 1-dimensional simplicial set, moreover an $\infty$-category (by virtue of being a \emph{simple} graph, with no multi-edges or loops). Hence there is a natural map, the inclusion, that takes $N(A)$ into $N(\mathcal Kan) = \mathcal S$.  Finally, Construction A.9.2 of Lurie describes a map that takes a functor from $A$-exit paths into spaces and gives back an $A$-constructible sheaf over $X$, which Theorem A.9.3 shows to be an equivalence, given the following conditions:

• $X$ is paracompact,
• $X$ is locally of singular shape,
• the $A$-stratification of $X$ is conical, and
• $A$ satisfies the ascending chain condition.

The first condition is satisfied as both $\Ran^{\leqslant n}(M)$ and $\R_{\geqslant 0}$ are locally compact and second countable. The last condition is satisfied because $A$ is a finite poset. We already mentioned that the conical property will be checked later, as will the singular shape property. Unfortunately, Lurie gives a definition of singular shape only for $\infty$-topoi, so some work must be done to translate this into our simpler setting. However, in the introduction to Appendix A, Lurie says that if $X$ is "sufficiently nice" and we assume some "mild assumptions" about $A$, then the described categorical equivalence follows, so it seems there is hope that everything will work out well in the end.

References: Stacks Project, Lurie (Higher algebra, Appendix A), Ayala, Francis and Tanaka (Local structures on stratified spaces, Sections 2 and 3)

Exit paths, part 1

This post is meant to set up all the necessary ideas to define the category of exit paths.

Preliminaries

 Let $X$ be a topological space and $C$ a category. Recall the following terms:

• $\Delta$: The category whose objects are finite ordered sets $[n]=(1,\dots,n)$ and whose morphisms are non-decreasing maps. It has several full subcategories, including
  • $\Delta_s$, comprising the same objects of $\Delta$ and only injective morphisms, and
  • $\Delta_{\leqslant n}$, comprising only the objects $[0],\dots,[n]$ with the same morphisms.
• equalizer: An object $E$ and a universal map $e:E\to X$, with respect to two maps $f,g:X\to Y$. It is universal in the sense that all maps into $X$ whose compositions with $f,g$ are equal factor through $e$. Equalizers and coequalizers are described by the diagram below, with universality given by existence of the dotted maps.

• fibered product or pullback: The universal object $X\times_Z Y$ with maps to $X$ and $Y$, with respect to maps $X\to Z$ and $Y\to Z$.
• fully faithful: A functor $F$ whose morphism restriction $\Hom(X,Y)\to \Hom(F(X),F(Y))$ is surjective (full) and injective (faithful).
• locally constant sheaf: A sheaf $\mathcal F$ over $X$ for which every $x\in X$ has a neighborhood $U$ such that $\mathcal F|_U$ is a constant sheaf. For example, constructible sheaves are locally constant on every stratum. 
• simplicial object: A contravariant functor from $\Delta$ to any other category. When the target category is $\text{Set}$, it is called a simplicial set. They may also be viewed as a collection $S = \{S_n\}_{\geqslant 0}$ for $S_n=S([n])$ the value of the functor on each $[n]$. Simplicial sets come with two natural maps:
  • face maps $d_i:S_n\to S_{n-1}$ induced by the map $[n-1]\to [n]$ which skips the $i$th piece, and
  • degeneracy maps $s_i:S_n\to S_{n+1}$ induced by the map $[n+1]\to[n]$ which repeats the $i$th piece.
• stratification: A property of a cover $\{U_i\}$ of $X$ for which consecutive differences $U_{i+1}\setminus U_i$ have ``nicer" properties than all of $X$. For example, $E_i\to U_{i+1}\setminus U_i$ is a rank $i$ vector bundle, but there is no vector bundle $E\to X$ that restricts to every $E_i$.

Now we get into new territory.

Definition: The nerve of a category $C$ is the collection $N(C) = \{N(C)_n = Fun([n],C)\}_{n\geqslant 0}$, where $[n]$ is considered as a category with objects $0,\dots,n$ and a single morphism in $\Hom_{[n]}(s,t)$ iff $s\leqslant t$.

Note that the nerve of $C$ is a simplicial set, as it is a functor from $\Delta^{op}\to Fun(\Delta,C)$. Moreover, the pieces $N(C)_0$ are the objects of $C$ and $N(C)_1$ are the morphisms of $C$, so all the information about $C$ is contained in its nerve. There is more in the higher pieces $N(C)_n$, so the nerve (and simplicial sets in general) may be viewed as a generalization of a category.

Kan structures

Let $\text{sSet}$ be the category of simplicial sets. We may consider $\Delta^n = \Hom_\Delta(-,[n])$ as a contravariant functor $\Delta\to \text{Set}$, so it is an object of $\text{sSet}$.

Definition: Fix $n\geqslant 0$ and choose $0\leqslant i\leqslant n$. Then the $i$th $n$-horn of a simplicial set is the functor $\Lambda^n_i\subset \Delta^n$ generated by all the faces $\Delta^n(d_j)$, for $j\neq i$.

We purposefully do not describe what "$\subset$" or "generated by" mean for functors, hoping that intuition fills in the gaps. In some sense the horn feels like a partially defined functor (though it is a true simplicial set), well described by diagrams, for instance with $n=2$ and $i=1$ we have

Definition: A simplicial set $S$ is a Kan complex whenever every map $f:\Lambda^n_i\to S$ factors through $\Delta^n$. That is, when there exists a

The map $\iota$ is the inclusion. Moreover, $S$ is an $\infty$-category, or quasi-category, if the extending map $f'$ is unique.

Example: Some basic examples of $\infty$-categories, for $X$ a topological space, are

• $Sing(X)$, made up of pieces $Sing(X)_n = \Hom(\Delta^n,X)$, and
• $LCS(X)$, the category of locally constant sheaves over $X$. Here $LCS(X)_n$ over an object $A$, whose objects are $B\to A$ and morphisms are the appropriate commutative diagrams

Definition: A morphism $p\in \Hom_{\text{sSet}}(S,T)$ is a Kan fibration if for every commutative diagram (of solid arrows)

the dotted arrow exists, making the new diagram commute.

Definition: Let $C,D,A$ be categories with functors $F:C\to D$ and $G:C\to A$.

• The left Kan extension of $F$ along $G$ is a functor $A\xrightarrow L D$ and a universal natural transformation $F\stackrel \lambda \rightsquigarrow L\circ G$.
• The right Kan extension of $F$ along $G$ is a functor $A\xrightarrow R D$ and a universal natural transformation $R\circ G \stackrel \rho\rightsquigarrow F$.

Exit paths

The setting for this section is constructible sheaves over a topological space $X$. We begin with a slightly more technical definition of a stratification.

Definition: Let $(A,\leqslant)$ be a partially ordered set with the upset topology. That is, if $x\in U$ is open and $x\leqslant y$, then $y\in A$. An $A$-stratification of $X$ is a continuous function $f:X\to A$.

We now begin with a Treumann's definition of an exit path, combined with Lurie's stratified setting.

Definition: An exit path in an $A$-stratified space $X$ is a continuous map $\gamma:[0,1]\to X$ for which there exists a pair of chains $a_1\leqslant \cdots \leqslant a_n$ in $A$ and $0=t_0\leqslant \cdots \leqslant t_n=1$ in $[0,1]$ such that $f(\gamma(t))=a_i$ whenever $t\in (t_{i-1},t_i]$.

This really is a path, and so gives good intuition for what is happening. Recall that the geometric realization of the functor $\Delta^n$ is $|\Delta^n| = \{(t_0,\dots,t_n)\in \R^{n+1}\ :\ t_0+\cdots+t_n=1\}$. Oserving that $[0,1]\cong|\Delta^1|$, Lurie's definition of an exit path is more general by instead considering maps from $|\Delta^n|$.

Definition: The category of exit paths in an $A$-stratified space $X$ is the simplicial subset $Sing^A(X)\subset Sing(X)$ consisting of those simplices $\gamma:|\Delta^n|\to X$ for which there exists a chain $a_0\leqslant \cdots \leqslant a_n$ in $A$ such that $f(\gamma(t_0,\dots,t_i,0,\dots,0))=a_i$ for $t_i\neq 0$.

Example: As with all new ideas, it is useful to have an example. Consider the space $X=\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$ of a closed manifold $M$ (see post "A constructible sheaf over the Ran space" 2017-06-24 for more). With the poset $(A,\leqslant)$ being $(a\leqslant b\leqslant c)$ and stratifying map
\[
\begin{array}{r c l}
f\ :\ X & \to & A, \\
(P,t) & \mapsto & \begin{cases}
a & \text{ if } P\in \Ran^1(M), \\
b & \text{ if } P\in \Ran^2(M), t\leqslant d(P_1,P_2), \\
c & \text{ else,}
\end{cases}
\end{array}
\]
we can make a continuous map $\gamma:\Delta^3\to X$ by
\[
\begin{array}{r c l}
(1,0,0) & \mapsto & (P\in \Ran^1(M),0), \\
(t_0,t_1\neq 0,0) & \mapsto & (P\in \Ran^2(M), d(P_1,P_2)), \\
(t_0,t_1,t_2\neq 0) & \mapsto & (P\in \Ran^2(M), t>d(P_1,P_2)).
\end{array}
\]
Then $f(\gamma(t_0\neq 0,0,0))=a$, and $f(\gamma(t_0,t_1\neq 0,0))=b$, and $f(\gamma(t_0,t_1,t_2\neq 0))=c$, as desired. The embedding of such a simplex $\gamma$ is described by the diagram below.

Both the image of $(1,0,0)$ and the 1-simplex from $(1,0,0)$ to $(0,1,0)$ lie in the singularity set of $\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$, which is pairs $(P,t)$ where $t=d(P_i,P_j)$ for some $i,j$. The idea that the simplex "exits" a stratum is hopefully made clear by this image.

References: Lurie (Higher algebra, Appendix A), Lurie (What is... an $\infty$-category?), Groth (A short course on $\infty$-categories, Section 1), Joyal (Quasi-categories and Kan complexes), Goerss and Jardine (Simplicial homotopy theory, Chapter 1), Treumann (Exit paths and constructible stacks)