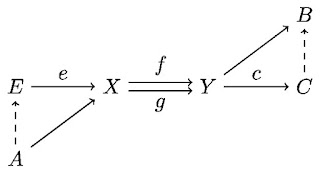A functor from entry paths to the nerve of simplicial complexes

Fix $n\in \Z_{>0}$ and let $X=\Ran^{\leqslant n}(M)\times \R_{>0}$ for $M$ a compact, connected PL manifold embedded in $\R^N$. Take $\widetilde h\colon X\to (B,\leqslant)$ the conical stratifying map from a previous post (``Conical stratifications via semialgebraic sets," 2018-04-16) compatible with the natural stratification $h\colon X\to SC$. The goal of this post is to construct a functor $F\colon \Sing_B(X) \to N(SC)$ from the $\infty$-category of entry paths that encodes the structure of $X$.

Recall that a simplicial set is a functor, an element of $\text{Fun}(\Delta^{op},\Set)$. A simplicial set $S$ is defined by its collection of $n$-simplices $S_n$, its face maps $s_i:S_{n-1}\to S_n$, and degeneracy maps $d_i:S_{n+1}\to S_k$, for all $i=0,\dots,n$. For the first simplicial set of interest in this post, we have
\begin{align*}
\Sing_B(X)_n & = \Hom_{\Top}^B(|\Delta^n|,X), \\
\left(s_i\colon [n]\to [n-1]\right) & \mapsto \left( \begin{array}{c}
\left(|\Delta^{n-1}|\to X \right) \mapsto \left(|\Delta^n|\to X\right) \\
\text{collapses $i$th with $(i+1)$th vertex, then maps as source}
\end{array}\right)\\
\left(d_i\colon [n]\to [n+1]\right) & \mapsto  \left(\begin{array}{c}
\left(|\Delta^{n+1}|\to X \right) \mapsto \left(|\Delta^n|\to X\right) \\
\text{maps as $i$th face of source map}
\end{array}\right)
\end{align*}
We write $\Hom^B_{\Top}$ for the subset of $\Hom_{\Top}$ that respects the stratification $B$ in the context of entry paths. For the second simplicial set, the nerve, we have
\begin{align*}
N(SC)_n & = \{(S_0\tov{f_1} \cdots \tov{f_n} S_n)\ :\ S_i\in SC,\ f_i\ \text{are simplicial maps}\}, \\
\left(s_i\colon [n]\to [n-1]\right) & \mapsto \left( \left(S_0\tov{f_1}\cdots \tov{f_{n-1}} S_{n-1} \right) \mapsto \left(S_0\tov{f_1} \cdots\tov{f_i} S_i \tov{\id} S_i\tov{f_{i+1}} \cdots \tov{f_{n-1}} S_{n-1}\right)\right),\\
\left(d_i\colon [n]\to [n+1]\right) & \mapsto \left(\begin{array}{r l}
i=0: & \left(S_0\cdots S_{n+1} \right) \mapsto \left(S_1\tov{f_2}\cdots \tov{f_{n+1}} S_{n+1} \right) \\
0<i<n: & \left(S_0 \cdots S_{n+1} \right) \mapsto \left(S_0\tov{f_1} \cdots\tov{f_{i-1}} S_{i-1} \tov{f_{i+1}\circ f_i} S_{i+1} \tov{f_{i+2}} \cdots \tov{f_{n+1}} S_{n+1}\right) \\
i=n: & \left(S_0 \cdots  S_{n+1} \right) \mapsto \left(S_0\tov{f_1}\cdots \tov{f_n} S_n \right)
\end{array} \right). 
\end{align*}
 Define $F$ on $k$-simplices as \[ F\left(\gamma\colon |\Delta^k|\to \Ran^{\leqslant n}(M)\times \R_{>0}\right) = \left(\widetilde h(\gamma(1,0,\dots,0)) \tov{\left(\widetilde h\circ \gamma \circ s_k\circ \cdots \circ s_2\right)\left( |\Delta^1|\right)} \cdots \tov{\left(\widetilde h\circ \gamma \circ s_{k-2}\circ \cdots \circ s_0\right)\left(|\Delta^1|\right)} \widetilde h(\gamma(0,\dots,0,1))\right). \] A morphism in $\Sing_B(X)$ is a composition of face maps $s_i$ and degeneracy maps $d_i$, so $F$ must satisfy the commutative diagrams

for all $s_i$, $d_i$. Since the maps are unwieldy when in coordinates, we opt for heuristic arguments, neglecting to trace out notation-heavy diagrams.

Commutativity of the diagram on the left is immediate, as considering a simplex $|\Delta^{n-1}|$ as the $i$th face of a larger simplex $|\Delta^n|$ is the same as adding a step that is the identity map in the Hamiltonian path of vertices of $|\Delta^{n-1}|$. Similarly, observing that the image of the shortest path $v_{i-1}\to v_i\to v_{i+1}$ in $|\Delta^{n+1}|$, for $v_i = (0,\dots,0,1,0,\dots,0)$ the $i$th standard basis vector, induced by an element $\gamma\colon |\Delta^{n+1}|\to X$ in $\Sing_B(X)_{n+1}$, is homotopic to the image of the shortest path $v_{i-1} \to v_{i+1}$ shows that the diagram on the right commutes. Since $F$ is a natural transformation between the two functors $\Sing_B(X)$ and $N(SC)$, it is a functor on the functors as simplicial sets.

Remark: The particular choice of $X$ did not seem to play a large role in the arguments above. However, the stratifying map $\widetilde h\colon X\to B$ has image sitting inside $SC$, the nerve of which is the target of $F$, and every morphism in $\Sing_B(X)$ can be interpreted as a relation in $B\subseteq SC$ (both were necessary for the commutativity of the diagrams). Hence it is not unreasonable to expect a similar functor $\Sing_A(X)\to N(A')$ may exist for a stratified space $X\to A\subseteq A'$.

Artin gluing a sheaf 4: a single sheaf in two ways

The goal of this post is to give an alternative perspective on making a sheaf over $X = \Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$, alternative to that of a previous post ("Artin gluing a sheaf 3: the Ran space," 2018-02-05). We will have one unique sheaf on all of $X$, valued either in simplicial complexes or simplicial sets.

Remark: Here we straddle the geometric category $SC$ of simplicial complexes and the algebraic category $\sSet$ of simplicial sets. There is a functor $[\ \cdot\ ]:SC\to \sSet$ for which every $n$-simplex in $S$ gets $(n+1)!$ elements in $[S]$, representing all the ways of ordering the vertices of $S$ (which we would like to view as unordered, to begin with).

Recall from previous posts:

• maps $f:X\to SC$ and $g = [f]:X\to \sSet$,
• the $SC_k$-stratification of $\Ran^k(M)\times \R_{\geqslant 0}$,
• the point-counting stratification of $\Ran^{\leqslant n}(M)$,
• the combined (via the product order) $SC_{\leqslant n}$-stratification of $\Ran^{\leqslant n}(M)\times \R_{\geqslant 0}$,
• an induced (by the $SC_k$-stratification) cover by nested open sets $B_{k,1},\dots,B_{k,N_k}$ of $\Ran^k(M)\times \R_{\geqslant 0}$,
• a corresponding induced total order $S_{k,1},\dots,S_{k,N_k}$ on $f(\Ran^k(M)\times \R_{\geqslant0})$.

The product order also induces a cover by nested opens of all of $X$ and a total order on $f(X)$ and $g(X)$. We call a path $\gamma:I\to X$ a descending path if $t_1<t_2\in I$ implies $h(\gamma(t_1))\geqslant h(\gamma(t_2))$ in any stratified space $h:X\to A$. Below, $h$ is either $f$ or $g$.

Lemma: A descending path $\gamma:I\to X$ induces a unique morphism $h(\gamma(0))\to h(\gamma(1))$.

Proof: Write $\gamma(0) = \{P_1,\dots,P_n\}$ and $\gamma(1) = \{Q_1,\dots,Q_m\}$, with $m\leqslant n$. Since the path is descending, points can only collide, not split. Hence $\gamma$ induces $n$ paths $\gamma_i:I\to M$ for $i=1,\dots,n$, with $\gamma_i$ the path based at $P_i$. This induces a map $h(\gamma(0))_0\to h(\gamma(1))_0$ on 0-cells (vertices or 0-objects), which completely defines a map $h(\gamma(0))\to h(\gamma(1))$ in the desired category. $\square$

Our sheaves will be defined using colimits. Fortunately, both $SC$ and $\sSet$ have (small) colimits. Finally, we also need an auxiliary function $\sigma:\Op(X)\to SC$ that finds the correct simplicial complex. Define it by \[ \sigma(U)  = \begin{cases}
S_{k,\ell} & \text{ if } U\neq\emptyset, \text{ for } k = \max\{1\leqslant k'\leqslant n\ :\ U\cap \Ran^k(M)\times \R_{\geqslant 0}\neq \emptyset\}, \\ & \hspace{2.23cm} \ell = \max\{1\leqslant \ell'\leqslant N_k\ :\ U \cap B_{k,\ell'}\neq\emptyset\},\\
* & \text{ if }U= \emptyset.
\end{cases} \]

Proposition 1: Let $\mathcal F$ be the function $\Op(X)^{op}\to SC$ on objects given by \[ \mathcal F(U) = \colim\left(\sigma(U)\rightrightarrows S\ :\ \text{every }\sigma(U)\to S \text{ is induced by a descending }\gamma:I\to U\right). \] This is a functor and satisfies the sheaf gluing conditions.

Proof: We have a well-defined function, so we have to describe the restriction maps and show gluing works. Since $V\subseteq U\subseteq X$, every $S$ in the directed system defining $\mathcal F(V)$ is contained in the directed system defining $\mathcal F(U)$. As there are maps $\sigma(V)\to \mathcal F(V)$ and $S\to \mathcal F(V)$, for every $S$ in the directed system of $V$, precomposing with any descending path we get maps $\sigma (U)\to \mathcal F(V)$ and $S\to \mathcal F(V)$, for every $S$ in the directed system of $U$. Then universality of the colimit gives us a unique map $\mathcal F(U)\to \mathcal F(V)$. Note that if there are no paths (decending or otherwise) from $U$ to $V$, then the colimit over an empty diagram still exists, it is just the initial object $\emptyset$ of $SC$.

To check the gluing condition, first note that every open $U\subseteq X$ must nontrivially intersect $\Ran^n(M)\times \R_{\geqslant 0}$, the top stratum (in the point-counting stratification). So for $W = U\cap V$, if we have $\alpha\in \mathcal F(U)$ and $\beta \in \mathcal F(V)$ such that $\alpha|_W = \beta|_W$ is a $k$-simplex, then $\alpha$ and $\beta$ must have been $k$-simplices as well. This is because a simplicial takes a simplex to a simplex, and we cannot collide points while remaining in the top stratum. Hence the pullback of $S\owns \alpha$ and $T\owns \beta$ via some induced maps (by descending paths) from $U$ to $W$ and $V$ to $W$, respectively, will restrict to the identity on the chosen $k$-simplex. Hence the gluing condition holds, and $\mathcal F$ is a sheaf. $\square$

Functoriality of $[\ \cdot\ ]$ allows us to extend the proof to build a sheaf valued in simplicial sets.

Proposition 2: Let $\mathcal G$ be the function $\Op(X)^{op}\to \sSet$ on objects given by \[ \mathcal G(U) = \colim\left([\sigma(U)]\rightrightarrows S\ :\ \text{every }[\sigma(U)]\to S \text{ is induced by a descending }\gamma:I\to U\right). \] This is a functor and satisfies the sheaf gluing conditions.

Remark: The sheaf $\mathcal G$ is non-trivial on more sets. For example, any path contained within one stratum of $X$ induces the identity map on simplicial sets (though not on simplicial complexes). Hence $\mathcal G$ is non-trivial on every open set contained within a single stratum.

References: nLab (article "Simplicial complexes"), n-category Cafe (post "Simplicial Sets vs. Simplicial Complexes," 2017-08-19)

Artin gluing a sheaf 2: simplicial sets and configuration spaces

The goal of this post is to extend the previous stratifying map to simplicial sets, and to generalize the sheaf construction to $X = \Conf_n(M)\times \R_{\geqslant 0}$ for arbitrary integers $n$, where $M$ is a smooth, compact, connected manifold. We work with $\Conf_n(M)$ instead of $\Ran^{\leqslant n}(M)$ because Lemma 1 and Proposition 2 have no chance of extending to $\Ran^{\leqslant n}(M)$ without major modifications (see Remark 3 at the end of this post).

Recall $SC$ is the category of simplicial complexes and simplicial maps, with $SC_n$ the full subcategory of simplicial complexes on $n$ vertices. Our main function is \[ \begin{array}{r c c c l}
f\ :\ X & \tov{f_1} & SC & \tov{f_2} & \sSet, \\
(P,a) & \mapsto & VR(P,a) & \mapsto & \Hom_{\Set}(\Delta^\bullet,VR(P,a)).
\end{array} \] On $\Conf_n(M)$ we have a natural metric, the Hausdorff distance $d_H(P,Q) = \max_{p\in P}\min_{q\in Q}d(p,q)+\max_{q\in Q}\min_{p\in P}d(p,q)$. This induces the 1-product metric on $X$, as \[ d_X((P,a),(Q,b)) = d_H(P,Q) + d(a,b), \] where $d$ without a subscript is Euclidean distance. We could have chosen any other $p$-product metric, but $p=1$ makes computations easier. For a given $(P,t)\in X$, write $P = \{P_1,\dots,P_n\}$ and define its maximal neighborhood to be the ball $B_X(\min\{\delta_1,\delta_2,t\},P)$, where \[ \delta_1 = \min_{i<j}\{d(P_i,P_j)\},
\hspace{1cm}
\delta_2 = \min_{i<j}\{|d(P_i,P_j)-t|\ :\ d(P_i,P_j)\neq t\}. \]

Lemma 1: Any path $\gamma:I\to X$ induces a unique morphism $f(\gamma(0))\to f(\gamma(1))$ of simplicial sets.

Proof: Write $\gamma(0) = \{P_1,\dots,P_n\}$ and $\gamma(1) = \{Q_1,\dots,Q_n\}$. The map $\gamma$ induces $n$ paths $\gamma_i:I\to M$ for $i=1,\dots,n$, with $\gamma_i$ the path based at $P_i$. Let $s:\gamma(0)\to \gamma(1)$ be the map on simplicial complexes defined by $P_i\mapsto \gamma_i(1)$. Since we are in the configuration space, where points cannot collide (as opposed to the Ran space), this is a well-defined map. Then $f_2(s)$ is a morphism of simplicial complexes. $\square$

Note the morphism of simplicial sets induced by any path in a maximal neighborhood of $x\in X$ is the identity morphism. We now move to describing a sheaf over all of $X$.

Definition: Let $X$ be any topological space and $\mathcal C$ a category with pullbacks. Let $A\subseteq X$ open and $B=X\setminus A \subseteq X$ closed, with $i:A\hookrightarrow X$ and $j:B\hookrightarrow X$ the inclusion maps. Let $\mathcal F$ be a $\mathcal C$-valued sheaf on $A$ and $\mathcal G$ a $\mathcal C$-valued sheaf on $B$. Then the \emph{Artin gluing} of $\mathcal F$ and $\mathcal G$ is the $\mathcal C$-valued sheaf $\mathcal H$ on $X$ defined as the pullback, or fiber product, of $i_*\mathcal F$ and $j_*\mathcal G$ over $j_*j^*i_*\mathcal F$ in the diagram below.

Note the definition requires a choice of sheaf map $\varphi:\mathcal G\to j^*i_*\mathcal F$. In the proof below, this sheaf map will be the morphism of simplicial sets from Lemma 1 through the functor $\Hom_\Set(\Delta^\bullet,-) = f_2(-)$.

Recall the ordering of $SC_n$ described by the only definition in a previous post ("Exit paths, part 2," 2017-09-28). Fix a cover $\{A_i\}_{i=1}^{N}$ of $SC_n$ by nested open subsets (so $N=|SC_n|$), with $B_i := f_1^{-1}(A_i)$ and $B_{\leqslant i} := \bigcup_{j=1}^i B_i$. We now have an induced order on and cover of $\im(f)=\sSet'$, as a full subcategory of $\sSet$. Even more, we now have an induced total order on $\sSet' = \{S_1,\dots,S_N\}$, with $S_i$ the unique simplicial set in $A_i\setminus A_{i-1}$. For example, $S_1=\Hom_\Set(\Delta^\bullet,\Delta^n)$ and $S_{N}=\Hom_\Set(\Delta^\bullet,\bigcup_{i=1}^n\Delta^0)$.

For ease of notation, we let $B_0 = \emptyset$ and write $S_\emptyset = \Hom(\Delta^\bullet,\emptyset)$, $S_0 = \Hom(\Delta^\bullet,\Delta^0)$.

Definition 1: Let $\mathcal F_i:\Op(B_i)^{op}\to \sSet$ be the locally constant sheaf given by $\mathcal F_i(U_x) = S_i$, where $U_x$ is a subset of the maximal neighborhood of $x\in B_i$. In general, \[ \mathcal F_i(U) = \begin{cases}
S_i & \text{ if }\begin{array}[t]{l}U\neq \emptyset, \\U\text{ is path connected},\\\text{every loop }\gamma:I\to U\text{ induces }\id:f(\gamma(0))\to f(\gamma(1)),\end{array} \\
S_\emptyset & \text{ else if }U\neq\emptyset, \\
S_0 & \text{ else.}
\end{cases} \] In general, we say $U\subseteq X$ is good if it is non-empty, path connected, and every loop $\gamma:I\to U$ induces the identity morphism on simplicial sets.

Proposition 2: Let $\mathcal F_{\leqslant 1} = \mathcal F_1$, and $\mathcal F_{\leqslant i}$ be the sheaf on $B_{\leqslant i}$ obtained by Artin gluing $\mathcal F_i$ onto $\mathcal F_{\leqslant i-1}$, for all $i=2,\dots,N$. Then $\mathcal F = \mathcal F_{\leqslant N}$ is the $SC_n$-constructible sheaf on $X$ described by \[ \mathcal F(U) = \begin{cases}
S_{\max\{1\leqslant \ell\leqslant N\ :\ U\cap B_{\ell}\neq \emptyset\}} & \text{ if $U$ is good,}\\
S_\emptyset & \text{ else if }U\neq\emptyset, \\
S_0 & \text{ else.}
\end{cases} \hspace{2cm} (1) \]

Proof: We proceed by induction. Begin with the constant sheaf $\mathcal F_1$ on $B_1$ and $\mathcal F_2$ on $B_2$, which we would like to glue together to get a sheaf $\mathcal F_{\leqslant2}$ on $B_{\leqslant 2}$. Since $f_1$ is continuous in the Alexandrov topology on the poset $SC_{\leqslant n}$, $B_1\subseteq B_{\leqslant 2}$ is open and $B_2 \subseteq B_{\leqslant 2}$ is closed. Let $i:B_1\hookrightarrow B_{\leqslant 2}$ and $j:B_2\hookrightarrow B_{\leqslant 2}$ be the inclusion maps. The sheaf $j^*i_*\mathcal F_1$ has support $\closure(B_1)\cap B_2 \neq \emptyset$ with \[ j^*i_*\mathcal F_1(U) = \colim_{V\supseteq j(U)}\left[i_*\mathcal F_1(V)\right] = \colim_{V\supseteq U}\left[\mathcal F_1(V\cap B_1)\right] = \begin{cases}
S_1 & \text{ if }U\cap \closure(B_1)\text{ is good}, \\ S_\emptyset & \text{ else},
\end{cases} \] for any non-empty $U\subseteq B_2$. Let the sheaf map $\varphi:\mathcal F_2\to j^*i_*\mathcal F_1$ be the inclusion simplicial set morphism on good sets (it can be thought of as induced through Lemma 1 by a path starting in $U\cap B_2$ and ending in $V\cap B_1$, for $V$ a small enough set in the colimit above). Note that $S_2 = \Hom_\Set(\Delta^\bullet,\Delta^n\setminus \Delta^1)$, where $\Delta^n\setminus \Delta^1$ is the simplicial complex resulting from removing an edge from the complete simplicial complex on $n$ vertices. Let $\mathcal F_{\leqslant 2}$ be the pullback of $i_*\mathcal F_1$ and $j_*\mathcal F_2$ along $j_*j^*i_*\mathcal F_1$, and $U\subseteq B_{\leqslant 2}$ a good set. If $U\subseteq B_1$, then $\mathcal F_{\leqslant 2}(U) = \mathcal F_1(U)=S_1$, and if  $U\subseteq B_2$, then $\mathcal F_{\leqslant 2}(U) = \mathcal F_2(U) = S_2$. Now suppose that $U\cap B_1 \neq \emptyset$ but also $U\cap B_2\neq\emptyset$, which, since $U$ is good, implies that $U\cap \closure(B_1)\cap B_2\neq\emptyset$. Then we have the pullback square

If $U$ is not good, then the simplicial sets are $S_\emptyset$ or $S_0$, with nothing interesting going on. The pullback over a good set $U$ can be computed levelwise as \[ \mathcal F_{\leqslant 2}(U)_m = \{(\alpha,\beta)\in (S_1)_m\times (S_2)_m\ :\ \alpha=j_*\varphi(\beta)\}. \hspace{2cm} (2)\] Since $j_*\varphi$ is induced by the inclusion $\varphi$, it is the identity on its image. So $\alpha = j_*\varphi(\beta)$ means $\alpha=\beta$, or in other words, $\mathcal F_{\leqslant 2}(U)=S_2$. Hence for arbitrary $U\subseteq B_{\leqslant 2}$, we have \[ \mathcal F_{\leqslant 2}(U) = \begin{cases}
S_{\max\{\ell=1,2\ :\ U\cap B_{\ell}\neq \emptyset\}} & \text{ if $U$ is good,}\\
S_\emptyset & \text{ else if }U\neq\emptyset, \\
S_0 & \text{ else.}
\end{cases}\]

For the inductive step with $k>1$, let $\mathcal F_{\leqslant k}$ be the sheaf on $B_{\leqslant k}$ defined as in Equation (1), but with $k$ instead of $N$. We would like to glue $\mathcal F_{\leqslant k}$ to $\mathcal F_{k+1}$ on $B_{k+1}$ to get a sheaf $\mathcal F_{\leqslant k+1}$ on $B_{\leqslant k+1}$. As before, $B_k \subseteq B_{\leqslant k+1}$ is open and $B_{k+1}\subseteq B_{\leqslant k+1}$ is closed. For $i:B_k\hookrightarrow B_{\leqslant k+1}$ and $j:B_{k+1}\hookrightarrow B_{\leqslant k+1}$ the inclusion maps, the sheaf $j^*i_*\mathcal F_{\leqslant k}$ has support $\closure(B_{\leqslant k})\cap B_{k+1}$, with \[ j^*i_*\mathcal F_{\leqslant k}(U) = \colim_{V\supseteq j(U)}\left[i_*\mathcal F_{\leqslant k}(V)\right] = \colim_{V\supseteq U}\left[\mathcal F_{\leqslant k}(V\cap B_{\leqslant k})\right] = \begin{cases} S_{\max\{1\leqslant \ell\leqslant k\ :\ U\cap \closure(B_\ell)\neq\emptyset\}} & \text{ if }U\cap \closure(B_{\leqslant k})\text{ is good,} \\ S_\emptyset & \text{ else,} \end{cases} \] for any non-empty $U\subseteq B_{k+1}$. Let the sheaf map $\varphi:\mathcal F_{k+1}\to j^*i_*\mathcal F_{\leqslant k}$ be the inclusion simplicial set morphism on good sets (it can be thought of as induced through Lemma 1 by a path starting in $U\cap B_{k+1}$ and ending in $V\cap B_{\leqslant k}$, for $V$ a small enough set in the colimit above). For $U\subseteq B_{\leqslant k+1}$ a good set, if $U\subseteq B_{\leqslant k}$, then $\mathcal F_{\leqslant k+1}(U) = \mathcal F_{\leqslant k}(U)$, and if  $U\subseteq B_{k+1}$, then $\mathcal F_{\leqslant k+1}(U) = \mathcal F_{k+1}(U) = S_{k+1}$. Now suppose that $U\cap B_{\leqslant k} \neq \emptyset$ but also $U\cap B_{k+1}\neq\emptyset$, which, since $U$ is good, implies that $U\cap \closure(B_{\leqslant k})\cap B_{k+1}\neq\emptyset$. Then we have the pullback square

If $U$ is not good, then the simplicial sets are $S_\emptyset$ or $S_0$, with nothing interesting going on. Again, as in Equation (2), the pullback $\mathcal F_{\leqslant k+1}$ on a good set $U$ is \[ \mathcal F_{\leqslant k+1}(U)_m = \{(\alpha,\beta)\in (S_\ell)_m\times (S_{k+1})_m\ :\ \alpha = j_*\varphi(\beta)\}, \] and as before, this implies that $\mathcal F_{\leqslant k+1}(U) = S_{k+1}$. Hence $\mathcal F_{\leqslant k+1}$ is exactly of the form as in Equation (1), with $k+1$ instead of $N$, and by induction we get the desired description for $\mathcal F_{\leqslant N}= \mathcal F$.  $\square$

Remark 3: The statements given in this post do not extend to $\Ran^{\leqslant n}(M)$, at least not as stated. Lemma 1 fails if  somewhere along the path $\gamma$ a point splits in two or more points, as there is no canonical choice which of the "new" points should be the image of the "old" point. This means that the proof of Proposition 2 will also fail, because we relied on a uniquely defined sheaf map $\varphi$ between strata.

Next, we hope to use this approach to describe classic persistent homology results, and maybe link this to the concept of persistence modules.

References: Milne (Etale cohomology, Chapter 2.3)

Exit paths, part 1

This post is meant to set up all the necessary ideas to define the category of exit paths.

Preliminaries

 Let $X$ be a topological space and $C$ a category. Recall the following terms:

• $\Delta$: The category whose objects are finite ordered sets $[n]=(1,\dots,n)$ and whose morphisms are non-decreasing maps. It has several full subcategories, including
  • $\Delta_s$, comprising the same objects of $\Delta$ and only injective morphisms, and
  • $\Delta_{\leqslant n}$, comprising only the objects $[0],\dots,[n]$ with the same morphisms.
• equalizer: An object $E$ and a universal map $e:E\to X$, with respect to two maps $f,g:X\to Y$. It is universal in the sense that all maps into $X$ whose compositions with $f,g$ are equal factor through $e$. Equalizers and coequalizers are described by the diagram below, with universality given by existence of the dotted maps.

• fibered product or pullback: The universal object $X\times_Z Y$ with maps to $X$ and $Y$, with respect to maps $X\to Z$ and $Y\to Z$.
• fully faithful: A functor $F$ whose morphism restriction $\Hom(X,Y)\to \Hom(F(X),F(Y))$ is surjective (full) and injective (faithful).
• locally constant sheaf: A sheaf $\mathcal F$ over $X$ for which every $x\in X$ has a neighborhood $U$ such that $\mathcal F|_U$ is a constant sheaf. For example, constructible sheaves are locally constant on every stratum. 
• simplicial object: A contravariant functor from $\Delta$ to any other category. When the target category is $\text{Set}$, it is called a simplicial set. They may also be viewed as a collection $S = \{S_n\}_{\geqslant 0}$ for $S_n=S([n])$ the value of the functor on each $[n]$. Simplicial sets come with two natural maps:
  • face maps $d_i:S_n\to S_{n-1}$ induced by the map $[n-1]\to [n]$ which skips the $i$th piece, and
  • degeneracy maps $s_i:S_n\to S_{n+1}$ induced by the map $[n+1]\to[n]$ which repeats the $i$th piece.
• stratification: A property of a cover $\{U_i\}$ of $X$ for which consecutive differences $U_{i+1}\setminus U_i$ have ``nicer" properties than all of $X$. For example, $E_i\to U_{i+1}\setminus U_i$ is a rank $i$ vector bundle, but there is no vector bundle $E\to X$ that restricts to every $E_i$.

Now we get into new territory.

Definition: The nerve of a category $C$ is the collection $N(C) = \{N(C)_n = Fun([n],C)\}_{n\geqslant 0}$, where $[n]$ is considered as a category with objects $0,\dots,n$ and a single morphism in $\Hom_{[n]}(s,t)$ iff $s\leqslant t$.

Note that the nerve of $C$ is a simplicial set, as it is a functor from $\Delta^{op}\to Fun(\Delta,C)$. Moreover, the pieces $N(C)_0$ are the objects of $C$ and $N(C)_1$ are the morphisms of $C$, so all the information about $C$ is contained in its nerve. There is more in the higher pieces $N(C)_n$, so the nerve (and simplicial sets in general) may be viewed as a generalization of a category.

Kan structures

Let $\text{sSet}$ be the category of simplicial sets. We may consider $\Delta^n = \Hom_\Delta(-,[n])$ as a contravariant functor $\Delta\to \text{Set}$, so it is an object of $\text{sSet}$.

Definition: Fix $n\geqslant 0$ and choose $0\leqslant i\leqslant n$. Then the $i$th $n$-horn of a simplicial set is the functor $\Lambda^n_i\subset \Delta^n$ generated by all the faces $\Delta^n(d_j)$, for $j\neq i$.

We purposefully do not describe what "$\subset$" or "generated by" mean for functors, hoping that intuition fills in the gaps. In some sense the horn feels like a partially defined functor (though it is a true simplicial set), well described by diagrams, for instance with $n=2$ and $i=1$ we have

Definition: A simplicial set $S$ is a Kan complex whenever every map $f:\Lambda^n_i\to S$ factors through $\Delta^n$. That is, when there exists a

The map $\iota$ is the inclusion. Moreover, $S$ is an $\infty$-category, or quasi-category, if the extending map $f'$ is unique.

Example: Some basic examples of $\infty$-categories, for $X$ a topological space, are

• $Sing(X)$, made up of pieces $Sing(X)_n = \Hom(\Delta^n,X)$, and
• $LCS(X)$, the category of locally constant sheaves over $X$. Here $LCS(X)_n$ over an object $A$, whose objects are $B\to A$ and morphisms are the appropriate commutative diagrams

Definition: A morphism $p\in \Hom_{\text{sSet}}(S,T)$ is a Kan fibration if for every commutative diagram (of solid arrows)

the dotted arrow exists, making the new diagram commute.

Definition: Let $C,D,A$ be categories with functors $F:C\to D$ and $G:C\to A$.

• The left Kan extension of $F$ along $G$ is a functor $A\xrightarrow L D$ and a universal natural transformation $F\stackrel \lambda \rightsquigarrow L\circ G$.
• The right Kan extension of $F$ along $G$ is a functor $A\xrightarrow R D$ and a universal natural transformation $R\circ G \stackrel \rho\rightsquigarrow F$.

Exit paths

The setting for this section is constructible sheaves over a topological space $X$. We begin with a slightly more technical definition of a stratification.

Definition: Let $(A,\leqslant)$ be a partially ordered set with the upset topology. That is, if $x\in U$ is open and $x\leqslant y$, then $y\in A$. An $A$-stratification of $X$ is a continuous function $f:X\to A$.

We now begin with a Treumann's definition of an exit path, combined with Lurie's stratified setting.

Definition: An exit path in an $A$-stratified space $X$ is a continuous map $\gamma:[0,1]\to X$ for which there exists a pair of chains $a_1\leqslant \cdots \leqslant a_n$ in $A$ and $0=t_0\leqslant \cdots \leqslant t_n=1$ in $[0,1]$ such that $f(\gamma(t))=a_i$ whenever $t\in (t_{i-1},t_i]$.

This really is a path, and so gives good intuition for what is happening. Recall that the geometric realization of the functor $\Delta^n$ is $|\Delta^n| = \{(t_0,\dots,t_n)\in \R^{n+1}\ :\ t_0+\cdots+t_n=1\}$. Oserving that $[0,1]\cong|\Delta^1|$, Lurie's definition of an exit path is more general by instead considering maps from $|\Delta^n|$.

Definition: The category of exit paths in an $A$-stratified space $X$ is the simplicial subset $Sing^A(X)\subset Sing(X)$ consisting of those simplices $\gamma:|\Delta^n|\to X$ for which there exists a chain $a_0\leqslant \cdots \leqslant a_n$ in $A$ such that $f(\gamma(t_0,\dots,t_i,0,\dots,0))=a_i$ for $t_i\neq 0$.

Example: As with all new ideas, it is useful to have an example. Consider the space $X=\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$ of a closed manifold $M$ (see post "A constructible sheaf over the Ran space" 2017-06-24 for more). With the poset $(A,\leqslant)$ being $(a\leqslant b\leqslant c)$ and stratifying map
\[
\begin{array}{r c l}
f\ :\ X & \to & A, \\
(P,t) & \mapsto & \begin{cases}
a & \text{ if } P\in \Ran^1(M), \\
b & \text{ if } P\in \Ran^2(M), t\leqslant d(P_1,P_2), \\
c & \text{ else,}
\end{cases}
\end{array}
\]
we can make a continuous map $\gamma:\Delta^3\to X$ by
\[
\begin{array}{r c l}
(1,0,0) & \mapsto & (P\in \Ran^1(M),0), \\
(t_0,t_1\neq 0,0) & \mapsto & (P\in \Ran^2(M), d(P_1,P_2)), \\
(t_0,t_1,t_2\neq 0) & \mapsto & (P\in \Ran^2(M), t>d(P_1,P_2)).
\end{array}
\]
Then $f(\gamma(t_0\neq 0,0,0))=a$, and $f(\gamma(t_0,t_1\neq 0,0))=b$, and $f(\gamma(t_0,t_1,t_2\neq 0))=c$, as desired. The embedding of such a simplex $\gamma$ is described by the diagram below.

Both the image of $(1,0,0)$ and the 1-simplex from $(1,0,0)$ to $(0,1,0)$ lie in the singularity set of $\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$, which is pairs $(P,t)$ where $t=d(P_i,P_j)$ for some $i,j$. The idea that the simplex "exits" a stratum is hopefully made clear by this image.

References: Lurie (Higher algebra, Appendix A), Lurie (What is... an $\infty$-category?), Groth (A short course on $\infty$-categories, Section 1), Joyal (Quasi-categories and Kan complexes), Goerss and Jardine (Simplicial homotopy theory, Chapter 1), Treumann (Exit paths and constructible stacks)