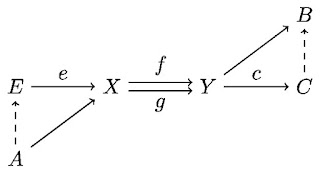This post is meant to set up all the necessary ideas to define the category of exit paths.
Now we get into new territory.
Definition: The nerve of a category $C$ is the collection $N(C) = \{N(C)_n = Fun([n],C)\}_{n\geqslant 0}$, where $[n]$ is considered as a category with objects $0,\dots,n$ and a single morphism in $\Hom_{[n]}(s,t)$ iff $s\leqslant t$.
Note that the nerve of $C$ is a simplicial set, as it is a functor from $\Delta^{op}\to Fun(\Delta,C)$. Moreover, the pieces $N(C)_0$ are the objects of $C$ and $N(C)_1$ are the morphisms of $C$, so all the information about $C$ is contained in its nerve. There is more in the higher pieces $N(C)_n$, so the nerve (and simplicial sets in general) may be viewed as a generalization of a category.
Let $\text{sSet}$ be the category of simplicial sets. We may consider $\Delta^n = \Hom_\Delta(-,[n])$ as a contravariant functor $\Delta\to \text{Set}$, so it is an object of $\text{sSet}$.
Definition: Fix $n\geqslant 0$ and choose $0\leqslant i\leqslant n$. Then the $i$th $n$-horn of a simplicial set is the functor $\Lambda^n_i\subset \Delta^n$ generated by all the faces $\Delta^n(d_j)$, for $j\neq i$.
We purposefully do not describe what "$\subset$" or "generated by" mean for functors, hoping that intuition fills in the gaps. In some sense the horn feels like a partially defined functor (though it is a true simplicial set), well described by diagrams, for instance with $n=2$ and $i=1$ we have
Definition: A simplicial set $S$ is a Kan complex whenever every map $f:\Lambda^n_i\to S$ factors through $\Delta^n$. That is, when there exists a
The map $\iota$ is the inclusion. Moreover, $S$ is an $\infty$-category, or quasi-category, if the extending map $f'$ is unique.
Example: Some basic examples of $\infty$-categories, for $X$ a topological space, are
Definition: A morphism $p\in \Hom_{\text{sSet}}(S,T)$ is a Kan fibration if for every commutative diagram (of solid arrows)
the dotted arrow exists, making the new diagram commute.
Definition: Let $C,D,A$ be categories with functors $F:C\to D$ and $G:C\to A$.
The setting for this section is constructible sheaves over a topological space $X$. We begin with a slightly more technical definition of a stratification.
Definition: Let $(A,\leqslant)$ be a partially ordered set with the upset topology. That is, if $x\in U$ is open and $x\leqslant y$, then $y\in A$. An $A$-stratification of $X$ is a continuous function $f:X\to A$.
We now begin with a Treumann's definition of an exit path, combined with Lurie's stratified setting.
Definition: An exit path in an $A$-stratified space $X$ is a continuous map $\gamma:[0,1]\to X$ for which there exists a pair of chains $a_1\leqslant \cdots \leqslant a_n$ in $A$ and $0=t_0\leqslant \cdots \leqslant t_n=1$ in $[0,1]$ such that $f(\gamma(t))=a_i$ whenever $t\in (t_{i-1},t_i]$.
This really is a path, and so gives good intuition for what is happening. Recall that the geometric realization of the functor $\Delta^n$ is $|\Delta^n| = \{(t_0,\dots,t_n)\in \R^{n+1}\ :\ t_0+\cdots+t_n=1\}$. Oserving that $[0,1]\cong|\Delta^1|$, Lurie's definition of an exit path is more general by instead considering maps from $|\Delta^n|$.
Definition: The category of exit paths in an $A$-stratified space $X$ is the simplicial subset $Sing^A(X)\subset Sing(X)$ consisting of those simplices $\gamma:|\Delta^n|\to X$ for which there exists a chain $a_0\leqslant \cdots \leqslant a_n$ in $A$ such that $f(\gamma(t_0,\dots,t_i,0,\dots,0))=a_i$ for $t_i\neq 0$.
Example: As with all new ideas, it is useful to have an example. Consider the space $X=\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$ of a closed manifold $M$ (see post "A constructible sheaf over the Ran space" 2017-06-24 for more). With the poset $(A,\leqslant)$ being $(a\leqslant b\leqslant c)$ and stratifying map
\[
\begin{array}{r c l}
f\ :\ X & \to & A, \\
(P,t) & \mapsto & \begin{cases}
a & \text{ if } P\in \Ran^1(M), \\
b & \text{ if } P\in \Ran^2(M), t\leqslant d(P_1,P_2), \\
c & \text{ else,}
\end{cases}
\end{array}
\]
we can make a continuous map $\gamma:\Delta^3\to X$ by
\[
\begin{array}{r c l}
(1,0,0) & \mapsto & (P\in \Ran^1(M),0), \\
(t_0,t_1\neq 0,0) & \mapsto & (P\in \Ran^2(M), d(P_1,P_2)), \\
(t_0,t_1,t_2\neq 0) & \mapsto & (P\in \Ran^2(M), t>d(P_1,P_2)).
\end{array}
\]
Then $f(\gamma(t_0\neq 0,0,0))=a$, and $f(\gamma(t_0,t_1\neq 0,0))=b$, and $f(\gamma(t_0,t_1,t_2\neq 0))=c$, as desired. The embedding of such a simplex $\gamma$ is described by the diagram below.
References: Lurie (Higher algebra, Appendix A), Lurie (What is... an $\infty$-category?), Groth (A short course on $\infty$-categories, Section 1), Joyal (Quasi-categories and Kan complexes), Goerss and Jardine (Simplicial homotopy theory, Chapter 1), Treumann (Exit paths and constructible stacks)
Preliminaries
Let $X$ be a topological space and $C$ a category. Recall the following terms:- $\Delta$: The category whose objects are finite ordered sets $[n]=(1,\dots,n)$ and whose morphisms are non-decreasing maps. It has several full subcategories, including
- $\Delta_s$, comprising the same objects of $\Delta$ and only injective morphisms, and
- $\Delta_{\leqslant n}$, comprising only the objects $[0],\dots,[n]$ with the same morphisms.
- equalizer: An object $E$ and a universal map $e:E\to X$, with respect to two maps $f,g:X\to Y$. It is universal in the sense that all maps into $X$ whose compositions with $f,g$ are equal factor through $e$. Equalizers and coequalizers are described by the diagram below, with universality given by existence of the dotted maps.
- fibered product or pullback: The universal object $X\times_Z Y$ with maps to $X$ and $Y$, with respect to maps $X\to Z$ and $Y\to Z$.
- fully faithful: A functor $F$ whose morphism restriction $\Hom(X,Y)\to \Hom(F(X),F(Y))$ is surjective (full) and injective (faithful).
- locally constant sheaf: A sheaf $\mathcal F$ over $X$ for which every $x\in X$ has a neighborhood $U$ such that $\mathcal F|_U$ is a constant sheaf. For example, constructible sheaves are locally constant on every stratum.
- simplicial object: A contravariant functor from $\Delta$ to any other category. When the target category is $\text{Set}$, it is called a simplicial set. They may also be viewed as a collection $S = \{S_n\}_{\geqslant 0}$ for $S_n=S([n])$ the value of the functor on each $[n]$. Simplicial sets come with two natural maps:
- face maps $d_i:S_n\to S_{n-1}$ induced by the map $[n-1]\to [n]$ which skips the $i$th piece, and
- degeneracy maps $s_i:S_n\to S_{n+1}$ induced by the map $[n+1]\to[n]$ which repeats the $i$th piece.
- stratification: A property of a cover $\{U_i\}$ of $X$ for which consecutive differences $U_{i+1}\setminus U_i$ have ``nicer" properties than all of $X$. For example, $E_i\to U_{i+1}\setminus U_i$ is a rank $i$ vector bundle, but there is no vector bundle $E\to X$ that restricts to every $E_i$.
Now we get into new territory.
Definition: The nerve of a category $C$ is the collection $N(C) = \{N(C)_n = Fun([n],C)\}_{n\geqslant 0}$, where $[n]$ is considered as a category with objects $0,\dots,n$ and a single morphism in $\Hom_{[n]}(s,t)$ iff $s\leqslant t$.
Note that the nerve of $C$ is a simplicial set, as it is a functor from $\Delta^{op}\to Fun(\Delta,C)$. Moreover, the pieces $N(C)_0$ are the objects of $C$ and $N(C)_1$ are the morphisms of $C$, so all the information about $C$ is contained in its nerve. There is more in the higher pieces $N(C)_n$, so the nerve (and simplicial sets in general) may be viewed as a generalization of a category.
Kan structures
Let $\text{sSet}$ be the category of simplicial sets. We may consider $\Delta^n = \Hom_\Delta(-,[n])$ as a contravariant functor $\Delta\to \text{Set}$, so it is an object of $\text{sSet}$.
Definition: Fix $n\geqslant 0$ and choose $0\leqslant i\leqslant n$. Then the $i$th $n$-horn of a simplicial set is the functor $\Lambda^n_i\subset \Delta^n$ generated by all the faces $\Delta^n(d_j)$, for $j\neq i$.
We purposefully do not describe what "$\subset$" or "generated by" mean for functors, hoping that intuition fills in the gaps. In some sense the horn feels like a partially defined functor (though it is a true simplicial set), well described by diagrams, for instance with $n=2$ and $i=1$ we have
Definition: A simplicial set $S$ is a Kan complex whenever every map $f:\Lambda^n_i\to S$ factors through $\Delta^n$. That is, when there exists a
The map $\iota$ is the inclusion. Moreover, $S$ is an $\infty$-category, or quasi-category, if the extending map $f'$ is unique.
Example: Some basic examples of $\infty$-categories, for $X$ a topological space, are
- $Sing(X)$, made up of pieces $Sing(X)_n = \Hom(\Delta^n,X)$, and
- $LCS(X)$, the category of locally constant sheaves over $X$. Here $LCS(X)_n$ over an object $A$, whose objects are $B\to A$ and morphisms are the appropriate commutative diagrams
Definition: A morphism $p\in \Hom_{\text{sSet}}(S,T)$ is a Kan fibration if for every commutative diagram (of solid arrows)
the dotted arrow exists, making the new diagram commute.
Definition: Let $C,D,A$ be categories with functors $F:C\to D$ and $G:C\to A$.
- The left Kan extension of $F$ along $G$ is a functor $A\xrightarrow L D$ and a universal natural transformation $F\stackrel \lambda \rightsquigarrow L\circ G$.
- The right Kan extension of $F$ along $G$ is a functor $A\xrightarrow R D$ and a universal natural transformation $R\circ G \stackrel \rho\rightsquigarrow F$.
Exit paths
The setting for this section is constructible sheaves over a topological space $X$. We begin with a slightly more technical definition of a stratification.
Definition: Let $(A,\leqslant)$ be a partially ordered set with the upset topology. That is, if $x\in U$ is open and $x\leqslant y$, then $y\in A$. An $A$-stratification of $X$ is a continuous function $f:X\to A$.
We now begin with a Treumann's definition of an exit path, combined with Lurie's stratified setting.
Definition: An exit path in an $A$-stratified space $X$ is a continuous map $\gamma:[0,1]\to X$ for which there exists a pair of chains $a_1\leqslant \cdots \leqslant a_n$ in $A$ and $0=t_0\leqslant \cdots \leqslant t_n=1$ in $[0,1]$ such that $f(\gamma(t))=a_i$ whenever $t\in (t_{i-1},t_i]$.
This really is a path, and so gives good intuition for what is happening. Recall that the geometric realization of the functor $\Delta^n$ is $|\Delta^n| = \{(t_0,\dots,t_n)\in \R^{n+1}\ :\ t_0+\cdots+t_n=1\}$. Oserving that $[0,1]\cong|\Delta^1|$, Lurie's definition of an exit path is more general by instead considering maps from $|\Delta^n|$.
Definition: The category of exit paths in an $A$-stratified space $X$ is the simplicial subset $Sing^A(X)\subset Sing(X)$ consisting of those simplices $\gamma:|\Delta^n|\to X$ for which there exists a chain $a_0\leqslant \cdots \leqslant a_n$ in $A$ such that $f(\gamma(t_0,\dots,t_i,0,\dots,0))=a_i$ for $t_i\neq 0$.
Example: As with all new ideas, it is useful to have an example. Consider the space $X=\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$ of a closed manifold $M$ (see post "A constructible sheaf over the Ran space" 2017-06-24 for more). With the poset $(A,\leqslant)$ being $(a\leqslant b\leqslant c)$ and stratifying map
\[
\begin{array}{r c l}
f\ :\ X & \to & A, \\
(P,t) & \mapsto & \begin{cases}
a & \text{ if } P\in \Ran^1(M), \\
b & \text{ if } P\in \Ran^2(M), t\leqslant d(P_1,P_2), \\
c & \text{ else,}
\end{cases}
\end{array}
\]
we can make a continuous map $\gamma:\Delta^3\to X$ by
\[
\begin{array}{r c l}
(1,0,0) & \mapsto & (P\in \Ran^1(M),0), \\
(t_0,t_1\neq 0,0) & \mapsto & (P\in \Ran^2(M), d(P_1,P_2)), \\
(t_0,t_1,t_2\neq 0) & \mapsto & (P\in \Ran^2(M), t>d(P_1,P_2)).
\end{array}
\]
Then $f(\gamma(t_0\neq 0,0,0))=a$, and $f(\gamma(t_0,t_1\neq 0,0))=b$, and $f(\gamma(t_0,t_1,t_2\neq 0))=c$, as desired. The embedding of such a simplex $\gamma$ is described by the diagram below.
Both the image of $(1,0,0)$ and the 1-simplex from $(1,0,0)$ to $(0,1,0)$ lie in the singularity set of $\Ran^{\leqslant 2}(M)\times \R_{\geqslant 0}$, which is pairs $(P,t)$ where $t=d(P_i,P_j)$ for some $i,j$. The idea that the simplex "exits" a stratum is hopefully made clear by this image.
References: Lurie (Higher algebra, Appendix A), Lurie (What is... an $\infty$-category?), Groth (A short course on $\infty$-categories, Section 1), Joyal (Quasi-categories and Kan complexes), Goerss and Jardine (Simplicial homotopy theory, Chapter 1), Treumann (Exit paths and constructible stacks)