The goal of this post is to understand when a map from a poset to an unordered set induces a partial order, and how that applies to the specific case of the set of simplicial complexes. Thanks to Yanlong Hao for spotting some mistakes in my seminar talk on the same topic yesterday.
Definition 1: Let $(A,\leqslant_A)$ be a poset and $f\colon A\to B$ a map of sets. The relation $\leqslant_B$ on $B$, with $a\leqslant_Aa'$ implying $f(a)\leqslant_Bf(a')$, is the relation induced by $f$ on $B$. The map $f$ is monotonic if whenever $b\leqslant_b b'$,
Lemma 2: If $f\colon A\to B$ is monotonic, then the induced relation $\leqslant_B$ is a partial order on $B$.
Proof: For reflexivity, take any $a\in A$, which has $a\leqslant_A a$ by reflexivity of $\leqslant_A$. Then $f(a)\leqslant_Bf(a)$, so every $b\in \im(f)$ satisfies reflexivity. Every $b\not\in\im(f)$ also satisfies reflexivity by the comment above.
For anti-symmetry, suppose that $b\leqslant_Bb'$ and $b'\leqslant_Bb$. Since $b\leqslant_B b'$, there is some $a\in f^{-1}(b)$ and $a'\in f^{-1}(b')$ such that $a\leqslant_A a'$. Similarly, there is some $c'\in f^{-1}(b')$ and $c\in f^{-1}(b)$ such that $c'\leqslant_A c$. Since $c\in f^{-1}(b)$ and $c'\in f^{-1}(b')$ are comparable, and the first assumed relation is $b\leqslant_Bb'$, by property 1 of Definition 1, we must have $c\leqslant_A c'$. By anti-symmetry of $A$, we now have that $c=c'$, so it follows that $b=f(c)=f(c')=b'$.
For transitivity, suppose that $b\leqslant_Bb'$ and $b'\leqslant_Bb''$. Take $a''\in f^{-1}(b'')$, for which property 2 of Definition 1 guarantees that there exists $a'\in f^{-1}(b')$ such that $a'\leqslant_Aa''$. Similarly, the first assumed relation and the same property guarantees there exists $a\in f^{-1}(b)$ such that $a\leqslant_Aa'$. By transitivity of $A$, we have $a\leqslant_A a''$. By the definition of $\leqslant_B$, we have $b=f(a) \leqslant_B f(a'') = b''$. $\square$
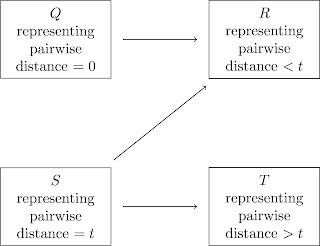
Let $M$ be a piecewise linear, compact, connected, embedded manifold in $\R^N$, and $SC$ the category of simplicial complexes. Let $A= \{1<2a>2b<3\}$. The product $A^N$ has the product order. Fix $n\in \Z_{>0}$ and let $T$ be the set of all distinct 2-,3-,...,$n$-tuples in $\{1,\dots,n\}$, or $T := \bigcup_{k=2}^n\left(\{1,\dots,n\}^k\setminus \Delta\right)/_{S_k}$. This set has size $\sum_{k=2}^n \binom nk = 2^n-n-1$. Assume every $v\in T$ is ordered in the canonical way. Then $v$ induces a natural projection $\pi_v\colon M^n \to M^{v}$, as well as another map \[ \begin{array}{r c l}
\pi_v'\colon M^n \times \R_{>0} & \to & A, \\
(P,t) & \mapsto & \begin{cases}
1 & \forall\ i,j, \pi_v(P)_i = \pi_v(P)_j, \\
2a & \exists\ i,j \text{ s.t. }\pi_v(P)_i\neq\pi_v(P)_j \text{ and } \textstyle\bigcap_{i=1}^{|v|} B(\pi_v(P)_i,t) \neq \emptyset, \\
2b & \exists\ i,j \text{ s.t. }\pi_v(P)_i\neq\pi_v(P)_j \text{ and } \textstyle\bigcap_{i=1}^{|v|} B(\pi_v(P)_i,t)=*, \\
3 & \exists\ i,j \text{ s.t. }\pi_v(P)_i\neq\pi_v(P)_j \text{ and } \textstyle\bigcap_{i=1}^{|v|} B(\pi_v(P)_i,t) = \emptyset.
\end{cases}
\end{array} \] Here all the balls $B$ are closed, and $M^n$ has the Hausdorff topology.
Lemma 3: The map $\pi_v$ is continuous on $M^v\times \R_{>0}$.
Proof: Every $(Q,s)\in (\pi_v')^{-1}(3)$ has an open ball of radius $\max_{i,j}\{d(\pi_v(Q)_i,\pi_v(Q)_j)\}/2-s$ around it that is still contained within $(\pi_v')^{-1}(3)$. Similarly, every $(Q,s)\in (\pi_v')^{-1}(2a)$ has an open ball of radius \[ \min\left\{\frac12\text{diam}\left(\bigcap_{i=1}^{|v|}B(\pi_v(Q)_i,s)\right),\max_{i,j}\{d(\pi_v(Q)_i,\pi_v(Q)_j)\}\right\} \hspace{2cm} (1) \] around it that is still contained within $(\pi_v')^{-1}(2a)$. The first expression in the $\min$ makes sure the intersection is non-empty, and the second expression makes sure all elements of $Q$ are not the same.
The set $(\pi_v')^{-1}(1<2a)$ is open by the same argument as for $2a\in A$, enlarging the open ball by removing the second expression in the $\min$ of expression (1). Finally, the set $(\pi_v')^{-1}(2a>2b<3)$ is open by the same argument, now enlarging the ball used for $2a\in A$ by removing the first expression in the $\min$ of expression (1). $\square$
Let $q\colon M^n\to \Ran^{\leqslant n}(M)$ be the natural quotient map, and $\check C\colon \Ran^{\leqslant n}(M)\times \R_{>0}\to SC$ be the Čech simplical complex map. For the next propositions, we will use two maps $f$ and $g$ defined as \[ \begin{array}{r c l}
f\colon M^n\times \R_{>0} & \to & A^{2^n-n-1}, \\
(P,t) & \mapsto & \prod_{v\in T} \pi_v'(P,t),
\end{array}
\hspace{2cm}
\begin{array}{r c l}
g\colon \im(f) & \to & SC, \\
f(P,t) & \mapsto & \check C(q(P),t).\end{array} \] The map $g$ is well-defined because $a\in A^{2^n-n-1}$ with non-empty preimage in $M^n\times \R_{>0}$ specifies whether or not every $k$-tuple of points has a simplex spanning it, for all $k=2,\dots,n$. This defines a unique simplicial complex, so choosing any $(P,t)\in f^{-1}(a)$ will give the same Čech complex, up to renaming of vertices.
Proposition: The map $f\colon M^n\times \R_{>0} \to A^{2^n-n-1}$ is continuous.
Proof: Let $a\in A^{2^n-n-1}$ and suppose that $f^{-1}(a)\neq \emptyset$. Let $a_i\in A$ be in the $i$th factor of $a$, and $r_i$ the radius of the open ball decreed by Lemma 3 to still be within $(\pi_v')^{-1}(a_i)$, where $v$ is the $i$th tuple in the chosen order on $T$. Then every $(P,t)\in f^{-1}(a)$ has an open ball of radius $\min_i\{r_i\}$ around it that is still contained within $f^{-1}(a)$, so $f$ is continuous. $\square$
Proposition: The map $g$ is monotonic.
Note that any relation $S\leqslant_{SC}S'$ may be split up as a chain of relations $S=T_1\leqslant_{SC} \cdots \leqslant_{SC} T_\ell=S'$, where the only differences between $T_i$ and $T_{i+1}$ are either (i) $T_i$ has a $k$-simplex $\sigma$ that $T_{i+1}$ does not have, or (ii) where $T_i$ has a single 0-simplex where a $k$-simplex $\sigma$ and all its faces used to be in $T_{i+1}$. Hence it suffices to show that properties 1 and 2 of Definition 1 are satisfied in cases (i) and (ii).
Proof: Case (i): Suppose that $S\leqslant_{SC}S'$, and take $a\in g^{-1}(S)$, $a'\in g^{-1}(S')$ with $a\leqslant_A a'$. If there is $b\in g^{-1}(S)$ and $b'\in g^{-1}(S')$ such that $b'\leqslant_A b$, then $g(b)$ has the $k$-simplex $\sigma$ that $g(b')$ does not have, but since $b'$ is ordered lower than $b$, it must be that this $k$-simplex has collapsed to a point. Then we would be in case (ii), a contradiction, so property 1 holds in this case.
Now let $i_1,\dots,i_{\sigma}$ be the indices of $a'$ and $a$ representing the $(k+1)$-fold intersection that describes $\sigma$, so $a'_j = 3$ and $a_j = 2b$ for all $j=i_1,\dots,i_\sigma$. Take any $b'\in g^{-1}(S')$, which also has some indices $\ell_1,\dots,\ell_\sigma$ representing this same $(k+1)$-fold intersection, so $b'_j=3$ at all $j=\ell_1,\dots,\ell_\sigma$. Let $b\in A^{2^n-n-1}$ be the element with all the same factors as $b'$, except at indices $\ell_1,\dots,\ell_\sigma$, which have been changed to $2b$. This element $b$ is still in $\im(f)$ as removing only this $k$-simplex still leaves the well-defined simplex $S'$ we assumed at the beginning. Hence $g(b)=S'$ and property 2 holds. \\
Case (ii): Suppose that $S\leqslant_{SC}S'$, and take $a\in g^{-1}(S)$, $a'\in g^{-1}(S')$ with $a\leqslant_A a'$. If there is $b\in g^{-1}(S)$ and $b'\in g^{-1}(S')$ such that $b'\leqslant_A b$, then $g(b')$ has the $k$-simplex $\sigma$ and all its faces that $g(b)$ does not have, but since $b'$ is ordered lower than $b$, it must be that we have introduced $\sigma$ and all its faces. Then we would be in case (i), or a chain of case (i) situations, a contradiction, so property \ref{1mon} holds in this case.
Now let $i_1,\dots,i_{\sigma}$ be the indices of $a'$ and $a$ representing the $(k+1)$-fold intersection that describes $\sigma$, and all the implied $(f+1)$-fold intersections that describe the $f$-faces of $\sigma$, $f>0$. That is, $a'_j = 2a$ and $a_j = 1$ for all $j=i_1,\dots,i_\sigma$. Take any $b'\in g^{-1}(S')$, which also has some indices $\ell_1,\dots,\ell_\sigma$ representing this same $(k+1)$-fold (and lower) intersection, so $b'_j=3$ at all $j=\ell_1,\dots,\ell_\sigma$. Let $b\in A^{2^n-n-1}$ be the element with all the same factors as $b'$, except at indices $\ell_1,\dots,\ell_\sigma$, which have been changed to $1$. This element $b$ is still in $\im(f)$ as collapsing this $k$-simplex and all its faces to a single 0-simplex still leaves the well-defined simplex $S'$ we assumed at the beginning. Hence $g(b)=S'$ and property 2 holds. $\square$
Since $g$ is monotonic, by Lemma 2 the relation $\leqslant_{SC}$ is a partial order on $SC$.
Definition 1: Let $(A,\leqslant_A)$ be a poset and $f\colon A\to B$ a map of sets. The relation $\leqslant_B$ on $B$, with $a\leqslant_Aa'$ implying $f(a)\leqslant_Bf(a')$, is the relation induced by $f$ on $B$. The map $f$ is monotonic if whenever $b\leqslant_b b'$,
- if $a\in f^{-1}(b)$, $a'\in f^{-1}(b)$ are comparable, then $a\leqslant_A a'$, and
- if $a'\in f^{-1}(b')$, then there exists $a\in f^{-1}(b)$ such that $a\leqslant_A a'$.
Lemma 2: If $f\colon A\to B$ is monotonic, then the induced relation $\leqslant_B$ is a partial order on $B$.
Proof: For reflexivity, take any $a\in A$, which has $a\leqslant_A a$ by reflexivity of $\leqslant_A$. Then $f(a)\leqslant_Bf(a)$, so every $b\in \im(f)$ satisfies reflexivity. Every $b\not\in\im(f)$ also satisfies reflexivity by the comment above.
For anti-symmetry, suppose that $b\leqslant_Bb'$ and $b'\leqslant_Bb$. Since $b\leqslant_B b'$, there is some $a\in f^{-1}(b)$ and $a'\in f^{-1}(b')$ such that $a\leqslant_A a'$. Similarly, there is some $c'\in f^{-1}(b')$ and $c\in f^{-1}(b)$ such that $c'\leqslant_A c$. Since $c\in f^{-1}(b)$ and $c'\in f^{-1}(b')$ are comparable, and the first assumed relation is $b\leqslant_Bb'$, by property 1 of Definition 1, we must have $c\leqslant_A c'$. By anti-symmetry of $A$, we now have that $c=c'$, so it follows that $b=f(c)=f(c')=b'$.
For transitivity, suppose that $b\leqslant_Bb'$ and $b'\leqslant_Bb''$. Take $a''\in f^{-1}(b'')$, for which property 2 of Definition 1 guarantees that there exists $a'\in f^{-1}(b')$ such that $a'\leqslant_Aa''$. Similarly, the first assumed relation and the same property guarantees there exists $a\in f^{-1}(b)$ such that $a\leqslant_Aa'$. By transitivity of $A$, we have $a\leqslant_A a''$. By the definition of $\leqslant_B$, we have $b=f(a) \leqslant_B f(a'') = b''$. $\square$
Let $M$ be a piecewise linear, compact, connected, embedded manifold in $\R^N$, and $SC$ the category of simplicial complexes. Let $A= \{1<2a>2b<3\}$. The product $A^N$ has the product order. Fix $n\in \Z_{>0}$ and let $T$ be the set of all distinct 2-,3-,...,$n$-tuples in $\{1,\dots,n\}$, or $T := \bigcup_{k=2}^n\left(\{1,\dots,n\}^k\setminus \Delta\right)/_{S_k}$. This set has size $\sum_{k=2}^n \binom nk = 2^n-n-1$. Assume every $v\in T$ is ordered in the canonical way. Then $v$ induces a natural projection $\pi_v\colon M^n \to M^{v}$, as well as another map \[ \begin{array}{r c l}
\pi_v'\colon M^n \times \R_{>0} & \to & A, \\
(P,t) & \mapsto & \begin{cases}
1 & \forall\ i,j, \pi_v(P)_i = \pi_v(P)_j, \\
2a & \exists\ i,j \text{ s.t. }\pi_v(P)_i\neq\pi_v(P)_j \text{ and } \textstyle\bigcap_{i=1}^{|v|} B(\pi_v(P)_i,t) \neq \emptyset, \\
2b & \exists\ i,j \text{ s.t. }\pi_v(P)_i\neq\pi_v(P)_j \text{ and } \textstyle\bigcap_{i=1}^{|v|} B(\pi_v(P)_i,t)=*, \\
3 & \exists\ i,j \text{ s.t. }\pi_v(P)_i\neq\pi_v(P)_j \text{ and } \textstyle\bigcap_{i=1}^{|v|} B(\pi_v(P)_i,t) = \emptyset.
\end{cases}
\end{array} \] Here all the balls $B$ are closed, and $M^n$ has the Hausdorff topology.
Lemma 3: The map $\pi_v$ is continuous on $M^v\times \R_{>0}$.
Proof: Every $(Q,s)\in (\pi_v')^{-1}(3)$ has an open ball of radius $\max_{i,j}\{d(\pi_v(Q)_i,\pi_v(Q)_j)\}/2-s$ around it that is still contained within $(\pi_v')^{-1}(3)$. Similarly, every $(Q,s)\in (\pi_v')^{-1}(2a)$ has an open ball of radius \[ \min\left\{\frac12\text{diam}\left(\bigcap_{i=1}^{|v|}B(\pi_v(Q)_i,s)\right),\max_{i,j}\{d(\pi_v(Q)_i,\pi_v(Q)_j)\}\right\} \hspace{2cm} (1) \] around it that is still contained within $(\pi_v')^{-1}(2a)$. The first expression in the $\min$ makes sure the intersection is non-empty, and the second expression makes sure all elements of $Q$ are not the same.
The set $(\pi_v')^{-1}(1<2a)$ is open by the same argument as for $2a\in A$, enlarging the open ball by removing the second expression in the $\min$ of expression (1). Finally, the set $(\pi_v')^{-1}(2a>2b<3)$ is open by the same argument, now enlarging the ball used for $2a\in A$ by removing the first expression in the $\min$ of expression (1). $\square$
Let $q\colon M^n\to \Ran^{\leqslant n}(M)$ be the natural quotient map, and $\check C\colon \Ran^{\leqslant n}(M)\times \R_{>0}\to SC$ be the Čech simplical complex map. For the next propositions, we will use two maps $f$ and $g$ defined as \[ \begin{array}{r c l}
f\colon M^n\times \R_{>0} & \to & A^{2^n-n-1}, \\
(P,t) & \mapsto & \prod_{v\in T} \pi_v'(P,t),
\end{array}
\hspace{2cm}
\begin{array}{r c l}
g\colon \im(f) & \to & SC, \\
f(P,t) & \mapsto & \check C(q(P),t).\end{array} \] The map $g$ is well-defined because $a\in A^{2^n-n-1}$ with non-empty preimage in $M^n\times \R_{>0}$ specifies whether or not every $k$-tuple of points has a simplex spanning it, for all $k=2,\dots,n$. This defines a unique simplicial complex, so choosing any $(P,t)\in f^{-1}(a)$ will give the same Čech complex, up to renaming of vertices.
Proposition: The map $f\colon M^n\times \R_{>0} \to A^{2^n-n-1}$ is continuous.
Proof: Let $a\in A^{2^n-n-1}$ and suppose that $f^{-1}(a)\neq \emptyset$. Let $a_i\in A$ be in the $i$th factor of $a$, and $r_i$ the radius of the open ball decreed by Lemma 3 to still be within $(\pi_v')^{-1}(a_i)$, where $v$ is the $i$th tuple in the chosen order on $T$. Then every $(P,t)\in f^{-1}(a)$ has an open ball of radius $\min_i\{r_i\}$ around it that is still contained within $f^{-1}(a)$, so $f$ is continuous. $\square$
Proposition: The map $g$ is monotonic.
Note that any relation $S\leqslant_{SC}S'$ may be split up as a chain of relations $S=T_1\leqslant_{SC} \cdots \leqslant_{SC} T_\ell=S'$, where the only differences between $T_i$ and $T_{i+1}$ are either (i) $T_i$ has a $k$-simplex $\sigma$ that $T_{i+1}$ does not have, or (ii) where $T_i$ has a single 0-simplex where a $k$-simplex $\sigma$ and all its faces used to be in $T_{i+1}$. Hence it suffices to show that properties 1 and 2 of Definition 1 are satisfied in cases (i) and (ii).
Proof: Case (i): Suppose that $S\leqslant_{SC}S'$, and take $a\in g^{-1}(S)$, $a'\in g^{-1}(S')$ with $a\leqslant_A a'$. If there is $b\in g^{-1}(S)$ and $b'\in g^{-1}(S')$ such that $b'\leqslant_A b$, then $g(b)$ has the $k$-simplex $\sigma$ that $g(b')$ does not have, but since $b'$ is ordered lower than $b$, it must be that this $k$-simplex has collapsed to a point. Then we would be in case (ii), a contradiction, so property 1 holds in this case.
Now let $i_1,\dots,i_{\sigma}$ be the indices of $a'$ and $a$ representing the $(k+1)$-fold intersection that describes $\sigma$, so $a'_j = 3$ and $a_j = 2b$ for all $j=i_1,\dots,i_\sigma$. Take any $b'\in g^{-1}(S')$, which also has some indices $\ell_1,\dots,\ell_\sigma$ representing this same $(k+1)$-fold intersection, so $b'_j=3$ at all $j=\ell_1,\dots,\ell_\sigma$. Let $b\in A^{2^n-n-1}$ be the element with all the same factors as $b'$, except at indices $\ell_1,\dots,\ell_\sigma$, which have been changed to $2b$. This element $b$ is still in $\im(f)$ as removing only this $k$-simplex still leaves the well-defined simplex $S'$ we assumed at the beginning. Hence $g(b)=S'$ and property 2 holds. \\
Case (ii): Suppose that $S\leqslant_{SC}S'$, and take $a\in g^{-1}(S)$, $a'\in g^{-1}(S')$ with $a\leqslant_A a'$. If there is $b\in g^{-1}(S)$ and $b'\in g^{-1}(S')$ such that $b'\leqslant_A b$, then $g(b')$ has the $k$-simplex $\sigma$ and all its faces that $g(b)$ does not have, but since $b'$ is ordered lower than $b$, it must be that we have introduced $\sigma$ and all its faces. Then we would be in case (i), or a chain of case (i) situations, a contradiction, so property \ref{1mon} holds in this case.
Now let $i_1,\dots,i_{\sigma}$ be the indices of $a'$ and $a$ representing the $(k+1)$-fold intersection that describes $\sigma$, and all the implied $(f+1)$-fold intersections that describe the $f$-faces of $\sigma$, $f>0$. That is, $a'_j = 2a$ and $a_j = 1$ for all $j=i_1,\dots,i_\sigma$. Take any $b'\in g^{-1}(S')$, which also has some indices $\ell_1,\dots,\ell_\sigma$ representing this same $(k+1)$-fold (and lower) intersection, so $b'_j=3$ at all $j=\ell_1,\dots,\ell_\sigma$. Let $b\in A^{2^n-n-1}$ be the element with all the same factors as $b'$, except at indices $\ell_1,\dots,\ell_\sigma$, which have been changed to $1$. This element $b$ is still in $\im(f)$ as collapsing this $k$-simplex and all its faces to a single 0-simplex still leaves the well-defined simplex $S'$ we assumed at the beginning. Hence $g(b)=S'$ and property 2 holds. $\square$
Since $g$ is monotonic, by Lemma 2 the relation $\leqslant_{SC}$ is a partial order on $SC$.